Inscription / Connexion Nouveau Sujet
Choix entre cos/sin
Bonjour,
voici mon problème qui se situe dans la dynamique : application de la 2ème loi de Newton.
J'aimerais comprendre comment choisir cos ou sin.
Par exemple dans le cas d'un plan incliné sans frottement ou on pousse un objet :
P + Rn + F = ma (en vecteur)
En projection sur Ox :
-mg sin α + F cos β = m ax
En projection sur Oy :
-mg cos α + Rn + F sin β = ay
Même si je pense que c'est toujours la même chose donc suffit d'apprendre par coeur (que sur Ox pour le poids c'est sin α...). je voudrais comprendre comment faire.
J'espère avoir été assez clair ^^ !
Cordialement
Bonjour,
Mauvais projet... Ce n'est pas quelque chose à apprendre "par cœur".
Il faut :
. faire un dessin
. chercher les triangles rectangles
. repérer les angles connus
. appliquer la trigonométrie
Exemple :
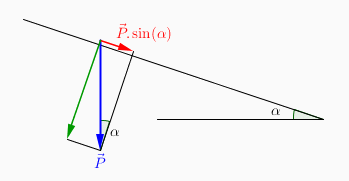
La composante du poids parallèlement au plan incliné vaut
.
La composante du poids perpendiculairement au plan incliné vaut
.

Voici un nouveau cas que j'ai du mal à comprendre : (voir schéma)
Je vais essayer d'expliquer
Pour la composante tangentielle de la traction je pense avoir compris :
C'est cosinus parce que : Adjacent/hypoténuse ce qui nous forme en effet l'angle Bêta
Mais pour la composante normale de la traction :
Pourquoi c'est sinus ?
Je crois qu'en plus d'avoir du mal à repérer les triangles rectangles, j'ai du mal à comprendre le principe et repérer les angles qu'on veux.
J'espère avoir été assez claire :/ Parce que je suppose que pour vous vous voyez tout de suite si c'est cosinus ou sinus et vous savez quelle angle "utiliser" non ?
Merci
Je reprends une partie de la figure :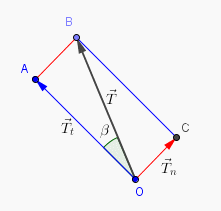
Il y a un rectangle (parallélogramme qui possède 4 angles droits et dont les côtés opposés ont, deux à deux, même longueur) : OABC
Tu as compris que
Le rectangle OABC te permet de conclure que
Or, dans le triangle rectangle OAB rectangle en A, on a
donc...
_________
Tu pourrais aussi considérer le triangle OBC rectangle en C.
et donc... même conclusion.
OK !!
En faite on utilise juste un triangle rectangle qui est identique à l'autre. (donc même angle...) et puis on "projette" !
Merci beaucoup !
Bonne journée


