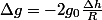Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. TerminaleForum de terminale PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau terminale
Partager :

Champs de gravitation

Posté par
JulienM 22-09-17 à 13:19

Bonjour ,
On nous a demandé de trouver une solution pour cette exercices mais après beacoup de tentative je n ai pas reussi .
Est ce que quelqu un peut m aider :
L exercice est :
(Pour des altitude h<<R
-Montrer que : g=ah+b et donner l expression de a et b

On peut utiliser la formule :
(1+x)^n ~ 1+nx si 0<x<<1)

C est ca l enoncé de l exercice , s il vous plait essayez de m aider dans ces deux jours

Posté par
diracre : Champs de gravitation 22-09-17 à 13:32

Hello

On va supposer que la Terre est une sphère de rayon R et de masse M.

1) peux tu rappeler l'expression générale de la force d'attraction que subit une masse m posée sur le sol? (donc à une altitude h = 0, ou bien  à une distance R du centre de la Terre)

2) cette force est le poids de la masse m que l'on écrit généralement  m\vec{g}

En comparant 1) et 2) peut tu détailler ce vecteur \vec{g}

3) Maintenant suppose que la masse m se situe à une altitude h, donc à une distance R' = R + h  du centre de la Terre. Exprime la force d'attraction subie par m.

4) Essaie d'exprimer cette force en fonction de \vec{g}

Arrivé là soit tu fais une pause, et propose tes résultats pour nous assurer que tout est OK, soit tu essaie de continuer tout seul

5) dans l'expression établie en 4) tu factorises R partout où tu le peux. Puis tu utilise la "formule" qui t'est donnée dans l'énoncé. Le résultat attendu devrait alors te tendre les bras

A toi ...

Posté par
JulienMre : Champs de gravitation 22-09-17 à 13:42

Voici la reponse que j ai trouve =
F=m.Mt.1/R'^2 .u(vecteur)

Posté par
diracre : Champs de gravitation 22-09-17 à 14:02

Presque ...  

(j'ai au passage légèrement adapté "mon" formalisme, qui n'est pas tout à fait celui de l'énoncé, pour plus de clarté je crois)

1)   \vec{F}=G \times \frac{m.M}{R^2}.\vec{u}  où \vec{u} est un vecteur unitaire dirigé vers le centre de la Terre

2) Donc on peut poser  \vec{F_0}= m \vec{g_0}   avec   \vec{g_0} =G \times \frac{M}{R^2}.\vec{u}  soit  g_0 =G \times \frac{M}{R^2}

3) La masse m est maintenant à R' = R + h du centre de la Terre

En ce point la force de gravitation est:

\vec{F_h}=G \times \frac{m.M}{R'^2}.\vec{u}

4) Faisons apparaitre g_0  et h  dans cette expression:

F_h=G \times \frac{m.M}{R'^2} = G \times \frac{m.M}{R^2} \times \frac{R^2}{R'^2}

Soit:

F_h= m \times G \times \frac{M}{R^2} \times \frac{R^2}{(R + h)^2}

Et donc:

F_h= m \times g_0 \times \frac{R^2}{R^2(1 + \frac{h}{R})^2}

Je te laisse poursuivre?

Posté par
JulienMre : Champs de gravitation 22-09-17 à 15:53

Merci pour ta réponse
Voila ce que j ai comme resultat:

1+2h/R = g0/g

Qu est ce que je dois faire apres

Posté par
diracre : Champs de gravitation 22-09-17 à 17:34

F_h= m \times g_h = m \times g_0 \times \frac{R^2}{R^2(1 + \frac{h}{R})^2}

Donc   g_h =  g_0 \times \frac{R^2}{R^2(1 + \frac{h}{R})^2}

Donc   g_h =  g_0 \times (1 + \frac{h}{R})^{-2}

Avec h <<R,  on fait un développement limité d'ordre 1 (la "formule" de l'énoncé)

Donc   g_h =  g_0 \times (1  -2 \frac{h}{R})

donc   g_h = ah + b   avec     b = g_0   et   a = -\frac{2g_0}{R}

On a bon?  

Posté par
JulienMre : Champs de gravitation 22-09-17 à 17:35

Merciiii 😍😍

Posté par
diracre : Champs de gravitation 22-09-17 à 18:12

Mon conseil.

Tu prends une page blanche et tu refais l'exercice.

- si ok tu passes à autre chose
- si pas ok, tu relis, puis tu reviens à l'étape page blanche

Si au bout de 3 fois tu ne t'en sors toujours pas en étant certain d'avoir "compris", tu reviens ici et tu racontes ce qui coinces .  On trouvera l'outil qu'il faut pour décoincer

Posté par
JulienMre : Champs de gravitation 22-09-17 à 18:14

Merci pour le conseil mais vu que j ai connu le principe je m en sors toujours

Posté par
diracre : Champs de gravitation 22-09-17 à 18:55

Alors ... pourquoi devrais je m'inquiéter ...

Posté par
atarikre : Champs de gravitation 22-09-17 à 19:50

ma reponse

** image supprimée **

Posté par
diracre : Champs de gravitation 22-09-17 à 20:03

Hello Atarik

Euh ... h est définie comme "altitude" (distance par rapport au sol donc) et non pas comme distance par apport au centre de la Terre  

Posté par
atarikre : Champs de gravitation 22-09-17 à 20:22

j ai vu h<R
dans ce cas que veut dire par la variable R
est ce que la variable R represente le rayon de terre?

Posté par
diracre : Champs de gravitation 22-09-17 à 22:13

R est bien le rayon terrestre

La fait que h (l'altitude) soit très inférieure au rayon terrestre (h << R) autorise le développement limité à l'ordre 1:

(1 + \frac{h}{R})^{-2} = 1 - 2\frac{h}{R}

Posté par
JulienMre : Champs de gravitation 22-09-17 à 22:34

Bonjour ,
S il vous plait dans le meme exercice on a une deuxieme question :

Jusqu'a quelle hauteur peut on considerer que g~g0 à 3% on donne r=6400km

Merci de me repondre

Posté par
atarikre : Champs de gravitation 22-09-17 à 23:33

OK

** image supprimée **

Posté par
JulienMre : Champs de gravitation 22-09-17 à 23:36

J ai besoin de la deuxieme question pour la premier j ai utilise les deux methodes

Posté par
atarikre : Champs de gravitation 22-09-17 à 23:40

3% de g  zero

** image supprimée => on recopie des formules **

Posté par
JulienMre : Champs de gravitation 22-09-17 à 23:48

J ai deja eu cette reponse mais ce n est pas logique car h est negligable devant r et ici elle est egale a 3000km

Posté par
diracre : Champs de gravitation 23-09-17 à 03:34

Hello

Ce n'est pas logique en effet car il y a une petite coquille je le crains dans ce qu'écrit Atarik:

Nous avions

g =  g_0 \times (1  -2 \frac{h}{R})

donc:

\Delta g = -2g_0\frac{\Delta h}{R}  

Soit

\Delta h = -\frac{R}{2}\frac{\Delta g}{g_0}

Une perte de 3% du poids correspond à une élévation d'altitude d'environ 96 km.

Posté par
diracre : Champs de gravitation 23-09-17 à 03:44

Au fait ...

Citation :
pour la premier j ai utilise les deux methodes


C'est quoi la 2eme méthode? Je n'en vois qu'une dans ce qui est exposé plus haut

Posté par
JulienMre : Champs de gravitation 23-09-17 à 12:49

La deuxieme methode est supprime
Je n ai pas compris comment vous avez fait pour avoir 96km

Posté par
diracre : Champs de gravitation 23-09-17 à 12:56

Citation :
La deuxieme methode est supprime
Je n ai pas compris comment vous avez fait pour avoir 96km


Euh ...

Si tu d'accord avec l'expression littérale que je te proposais ci dessus:   \Delta h = -\frac{R}{2}\frac{\Delta g}{g_0}

Tu fais juste le calcul numérique:   \Delta h = \frac{6371}{2}\times 0,03 \approx 96 km

Posté par
JulienMre : Champs de gravitation 23-09-17 à 12:59

C est ce que je ne comprend pas

Champs de gravitation

Posté par
diracre : Champs de gravitation 23-09-17 à 13:08

Aïe ... c'est plus sérieux que je ne l'espérais ...

Avais tu compris le résultat:   g_h =  g_0 \times (1  -2 \frac{h}{R})  

Si oui:

g_{h=0} = g_0

g_h =  g_0 \times (1  -2 \frac{h}{R})  

g_h - g_{h=0} = g_0 \times (1  -2 \frac{h}{R})  - g_0

Donc

g_h - g_{h=0} =   -2 g_0\frac{(h - 0)}{R})

Donc

\Delta g =   -2 g_0\frac{\Delta h}{R}

Est ce plus clair maintenant?

Posté par
JulienMre : Champs de gravitation 23-09-17 à 13:09

Je te remerci enormement pour l aide

Posté par
diracre : Champs de gravitation 23-09-17 à 13:32

Ouf ... la Terre est sauvée

N'hésite pas à répéter la résolution de ce problème sur "une page blanche" jusqu'à maitriser complètement le raisonnement et les étapes de calcul  (conseil d'ancien, qui tient ce conseil de ses anciens à lui, qui eux même ...)


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !