Inscription / Connexion Nouveau Sujet
Champ magnétique, solénoïde non horizontale
Bonjour, un énoncé me pose problème :
Plaçons une boussole horizontale au centre d'un solénoïde d'axe horizontal. Quand un courant électrique circule dans le solénoïde, l'aiguille de la boussole dévie de 20° vers l'est (cas n°1). En inversant le sens du courant, l'aiguille dévie de 70° vers l'ouest (cas n°2).
Quelle est la valeur de l'angle entre l'axe du solénoïde et la direction nord-sud ?
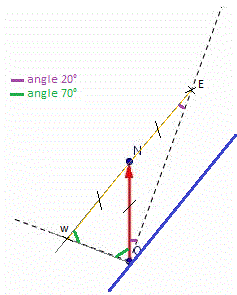
J'ai fais un schéma afin de matérialiser la situation, si je comprends bien on cherche l'angle violet ?
J'ai trouvé comme résultat d'angle recherché beta= 35 ° mais on raisonnement me semble un peu hasardeux, pouvez vous m'indiquer la marche à suivre ?
Merci
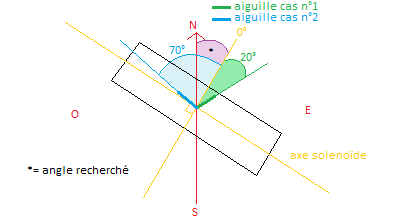
Bonjour,
Drôle de titre... le solénoïde a bien un axe horizontal.
Le dessin n'est pas bon.
Avant d'être déviée par le champ créé par le solénoïde (donc avant que le courant passe dans le solénoïde) l'aiguille de la boussole est orientée vers le nord...
Il va falloir :
1) tenir un raisonnement physique
2) faire appel à de vieux souvenirs de géométrie...
Je souhaite te lire sur la physique. Pour la géométrie, si c'est vraiment trop éloigné, je t'aiderai.

D'un point de vue physique on peut dire qu'avant que le courant ne se lance, la boussole pointe sur le pôle nord magnétique de la Terre. Une fois que le courant est lancé l'aiguille se comporte comme la résultante du champ magnétique terrestre et celui de la bobine. Plus l'intensité du courant est grande et plus l'aiguille se déportera vers l'axe du solénoïde. Si le solénoïde était perpendiculaire a l'axe nord sud de la terre, le courant gardant la même intensité mais changeant de sens, l'aiguille se déporterais sois vers l'est, soit vers l'ouest mais en gardant un angle de même valeur avec l'axe nord sud de la Terre.
Dans notre exercice, le solénoïde n'est pas perpendiculaire au fameux axe nord sud. L'angle d'inclinaison de l'aiguille s'en retrouve modifié et n'a pas la même valeur s'il se déporte a l'est ou a l'ouest vu que d'un côté il fais un angle de 20 et de l'autre côté un angle de 70 par rapport a l'axe nord sud.
Très bien !
Les deux informations que j'attendais :
Une fois que le courant est lancé l'aiguille se comporte comme la résultante du champ magnétique terrestre et celui de la bobine.
Oui, l'aiguille se dirige selon le champ magnétique résultant (somme vectorielle) du champ magnétique terrestre et du champ magnétique créé par le solénoïde.
L'autre information :
Si le solénoïde était perpendiculaire a l'axe nord sud de la terre, le courant gardant la même intensité mais changeant de sens, l'aiguille se déporterais sois vers l'est, soit vers l'ouest mais en gardant un angle de même valeur avec l'axe nord sud de la Terre.
Quand le courant dans le solénoïde change de sens, le champ créé garde la même direction (celle de l'axe du solénoïde), change de sens et garde la même intensité.
Un schéma :
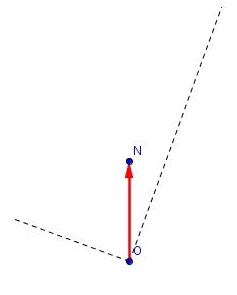
Le point O est le centre du solénoïde. C'est là que se trouve le pivot autour duquel tourne l'aiguille de la boussole.
La direction ON est la direction Sud-Nord. Le vecteur rouge est l'illustration du champ magnétique terrestre.
Le dessin est fait en l'absence de courant, donc en l'absence de champ magnétique créé par le solénoïde. Je n'ai pas représenté l'aiguille de la boussole, mais elle serait alignée sur cette direction Sud-Nord, la direction ON.
Les lignes en pointillé sont les lignes à 20° vers l'Est et à 70° vers l'ouest. L'énoncé dit que l'aiguille s'oriente selon ces directions quand le courant passe dans un sens puis dans le sens opposé.
Problème (de géométrie) :
Quelle est la direction commune (celle de l'axe du solénoïde) aux deux vecteurs qui représenteront les champs magnétiques créés par le solénoïde, vecteurs de même longueur (les champs magnétiques ont même intensité quand le courant change de sens), vecteurs d'origine commune le point N, telle que les extrémités de ces vecteurs se trouvent sur les lignes en pointillé ?
Aide : il ne t'a pas échappé que 20° + 70° = 90°
Un angle droit, en géométrie, cela peut s'avérer fort utile. Avec la présence d'un triangle rectangle par exemple...
Dis-moi sincèrement si tu te souviens des propriétés de géométrie de la classe de quatrième.

Pythagore avec SOH CAH TOA pas de problèmes
Et thales avec hypothènuse au carre = côté 1 au carré + côté 2 au carré oui ok.

Deux propriétés :
. L'hypoténuse d'un triangle rectangle est le diamètre du cercle circonscrit à ce triangle.
. Dans un triangle rectangle, la médiane issue du sommet de l'angle droit est égale à la moitié de l'hypoténuse.

Ce qui prouve, s'il en était besoin...
. que la physique n'est pas une question de "formule"
. mais que notre physique est bien liée aux mathématiques, ici la géométrie.
Je repense à la très célèbre phrase de Galilée et, en en cherchant les références, je tombe sur cette superbe conférence : 
![]()
Pour ceux qui aiment la philosophie des sciences !

Et si on aime pas la langouste ? 
Je n'arrive pas bien a comprendre l'utilité de ces formules pour notre cas précis. Pour savoir quelle formule utiliser il faut d'abord avoir un schéma précis dans la tête. Je n'arrive pas a visualiser le solénoïde
On cherche comment orienter deux vecteurs égaux et opposés (donc colinéaires), de même origine N de manière telle que l'extrémité de l'un soit sur la demi-droite 20°-est et que l'extrémité de l'autre soit sur la demi-droite 70°-ouest.
Le support commun à ces deux vecteurs sera parallèle à l'axe du solénoïde qui passe par le point O
Les deux vecteurs égaux et opposés représentent le champ magnétique créé par le solénoïde pour un sens du courant et pour l'autre.
Trace une droite passant par le point N.
Elle coupe les demi-droites 20°-est et 70°-ouest en deux points E et W
Est-ce que NE = NW ?
Si oui, tu as trouvé
Sinon, il faut une autre droite...
Comment ne pas tâtonner (car il y a une infinité de droite passant par le point N) ? Par la géométrie...

Bonjour coll
J'ai réussi à faire ce schéma avec un téléphone car pas de pc de dispo.
La droite en noir représente l'axe du solénoïde...
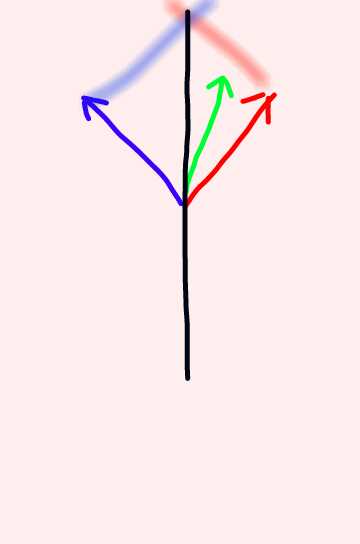
Ensuite concernant les points E et W je trouve ceci : (voir schéma) mais il y a quelque chose de faux je pense dans mon schéma car les points N et E sont confondus 
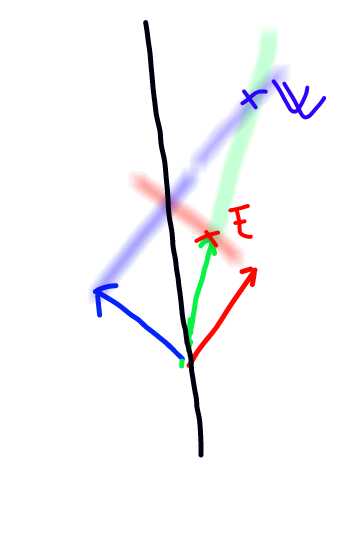
Sans commentaire et sans avoir nommé les points et les vecteurs, tes figures sont difficiles à interpréter.
Je ne pense pas que ce soit cela tant la différence est grande avec ce que j'attends.
_____________
Où doit se trouver le point E ?
. il doit être sur la ligne (en pointillés sur mon schéma) incliné de 20° vers l'est par rapport au nord
. il doit résulter de la somme vectorielle de deux vecteurs
. le vecteur qui représente le champ magnétique terrestre
. le vecteur qui représente le champ magnétique créé par le solénoïde pour un sens du courant
Où doit se trouver le point W ?
. il doit être sur la ligne (en pointillés sur mon schéma) incliné de 70° vers l'ouest par rapport au nord
. il doit résulter de la somme vectorielle de deux vecteurs
. le vecteur qui représente le champ magnétique terrestre
. le vecteur qui représente le champ magnétique créé par le solénoïde pour l'autre sens du courant
Ce que l'on sait encore :
ces deux vecteurs ont même module, même direction mais des sens opposés
L'axe du solénoïde sera la parallèle à la direction des deux vecteurs et
passant par le point O

Bonjour coll désolé de répondre si tard mais j'ai toujours ce soucis de pc. je pense que la figure devrai donner ceci: (voir schéma)
j'ai rajouté la même distance ON à partir du point N vers E et de l'autre sens c'est à dire de N vers W.
Ainsi les vecteurs NE et NW sont égaux, de même direction mais de sens opposé.
La droite bleue est parallèle aux deux vecteurs et représente l'axe du solénoïde
tout cela est il correcte?
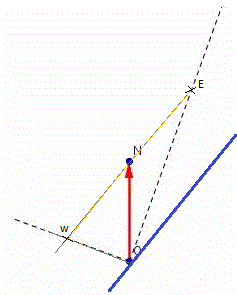
L'axe marron est perpendiculaire à l'axe du solénoïde.
j'utilise la fameuse formule qui dis que la somme des angles d'un triangle fait toujours 180° pour calculer l'angle jaune et en déduire l'angle rose recherché.
si angle rose est ALPHA, alors ALPHA = 40 °
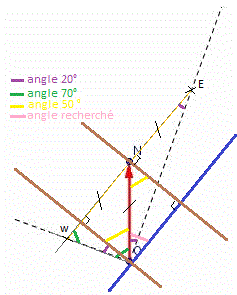

Tu as trouvé !
Puisque le champ magnétique créé par le solénoïde a même intensité qu'il soit dans un sens ou dans le sens opposé, on doit avoir :
NW = NE
donc le point N doit se trouver au milieu de l'hypoténuse à constuire.
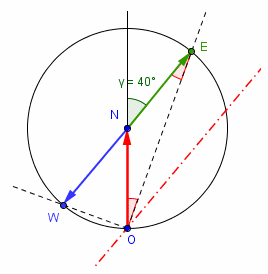
Mais alors ON sera la médiane issue du sommet de l'angle droit.
En conséquence NW = NE = ON
et les points W et E seront aux extrémités d'un diamètre du cercle de centre N, de rayon ON ; points d'intersection de ce cercle avec les droites à 20°-est et à 70°-ouest
L'axe du solénoïde passe par le point O et est parallèle à l'hypoténuse du triangle rectangle.
L'angle entre l'axe et la direction nord-sud, a même mesure que l'angle entre l'hypoténuse et la direction nord-sud.
On peut dire que la mesure de cet angle au centre vaut deux fois celle de l'angle inscrit correspondant
donc
On peut aussi dire que cet angle a pour mesure la somme des mesures des angles de base du triangle isocèle NEO, donc

On peut dire qu'il serai impossible que notre énoncé nous disent que l'angle 1 fasse 20 degrés et l'angle 2 fasse 50 degrés pour une même intensite mais dans un sens inverse ....
Si on change un peu l'énoncé et qu'on dis qu'on met une intensité I1 qui donne un angle alpha1, a notre aiguille sud nord, et dans le sens inverse une intensité I2 qui donne un angle aplha2, la géométrie ne nous sera plus d'aucune aide ? Seul le calcul pur et dur pourra nous aider c'est ça ?
Ok pour les explications coll je dois beaucoup a ile de physique, a toi et tout les autres 
En effet, tu réalises bien que ce petit miracle 20° + 70° = 90° n'est possible que parce que l'intensité du champ magnétique créé par le solénoïde est très exactement égale à l'intensité de la composante horizontale du champ magnétique terrestre.
Je ne me suis pas posé la question pour la résolution avec d'autres angles. Mais tu sais la géométrie a plus d'un tour dans son sac !
__________
Je t'en prie
À une prochaine fois !