Inscription / Connexion Nouveau Sujet
centre d inertie
Bonjour,
Enoncé :
Dans l'intention de recherche le niveau réel de ses élèves de terminal D ,le professeur de physique chimie de la classe présente le profil ci dessous d un jouet d enfant vu dans un super marché.
Pour l expérimentation du jouet M de masse m=1 kg,assimilable a un point matériel ,on le fait glisser sur la piste formée de deux parties AB et BC (voir figure) :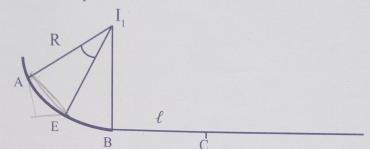
AB et BC sont dans le même plan vertical. AB représente 1/6 de circonférence de centre I1, et de rayon R=15 m.
Le point I1 est situé sur la piste verticale De B.BC est une partie rectiligne de longueur l=15 m.le jouet est propulsé en A par un dispositif de lancement , vers le bas , avec une vitesse initiale VA=6 m/s
La piste étant parfaitement lisse ,les frottements sur le jouet sont négligés le professeur demande a ses élèves de prouvée l existence des forces de frottements sur la piste AC.
Tu prends part a cette évaluation.
Questions :
1/ déterminer la vitesse VE au point E défini par l angle a =+I1A,I1A=pi/6
2/ déterminer la valeur de la réaction N de la piste sur le jouet au point E.
3/ la vitesse du jouet qu il existe au point C est VC=12,5 m/s.
3/1.montre qu il existe que les frottements sur la piste ne sont pas nuls.
3/2 déterminer l intensité de ces frottements assimilables a une force unique f tangente a la trajectoire d intensité f supposée constante.
***Edit gbm : topic aéré pour plus de lisibilité et image recadrée => pour la nième fois, merci de faire un effort là-dessus !***
Réponse
Question 1
Appliquons TEC
1/2 mVE^2-1/2mVA^2=W(P)+W(N) or w(N)=0
1/2 m(VE^2-VA^2)=mgh
VE^2-VB^2=2gh
VE=√2gh+VB^2
Déterminons la hauteur
Calculons l angle AI1B
On sait que une circonférence entière est 360
On aura
1/6*360=pi/3
AE=R-AI1
Considérons le triangle AI1K est rectangle en K
Cospi/3=AI1 /R
AI1=cos pi/3*R
AE=R(1-cospi/3)
VE=√2gr(1-cospi/3)+VA^2
VE=2*9,8*15(1-cospi/30)+36
VE=6,76 m/s^2
C est ça
Bonjour,
1/ déterminer la vitesse VE au point E défini par l angle a =+I1A,I1A=pi/6
Je ne comprends pas ce qui est surligné en bleu.
Ce que je n'ai pas compris ne se situe pas dans tes réponses ( que je n'ai pas encore lues) mais dans l'énoncé de la question 1 :
" 1/ déterminer la vitesse VE au point E défini par l angle a =+I1A,I1A=pi/6 "
Cette question définit un angle  comme étant l'angle que fait I1A avec .... I1A et qui serait égal à pi/6 soit à 30°
comme étant l'angle que fait I1A avec .... I1A et qui serait égal à pi/6 soit à 30°
Remarque :
Tes textes sont, le plus souvent, illisibles.
Merci, par exemple, pour le point I1 que tu écris I1 d'utiliser le bouton indice : x2
J'attends d'abord des explications sur ce mystérieux angle  entre I1A et I1A (Voir mon post du
entre I1A et I1A (Voir mon post du
04-11-19 à 20:26)
Il s'agit probablement d'une erreur de frappe.
Merci de la corriger.
Question 1
Appliquons TEC
1/2 mVE^2 - 1/2mVA^2=W(P)+W(N) or w(N)=0
1/2 m(VE^2-VA^2)=mgh
VE^2-VB^2=2gh Oui, mais il faut définir clairement ce qu'est " h "
VE=√( 2gh+VB^2)
Déterminons la hauteur
Calculons l angle A,I1,B
On sait que une circonférence entière est 360 degrés
On aura
1/6*360=pi/3
AE=R-AI1 Non
Considérons le triangle A,I1,K est rectangle en K Définir le point K
Cos (pi/3) =AI1 /R Non car AI1 = R
AI1=cos pi/3*R
AE=R(1-cospi/3)
VE=√2gr(1-cospi/3)+VA^2
VE=2*9,8*15(1-cospi/30)+36
VE=6,76 m/s^2 Non
Bonsoir
Question 1
Appliquons le théorème de l énergie cinétique
1/2mVE^2-1/2mVA^2=W(P)+W(N)
1/2m(VE^2-VA^2)=m*g*h et W(N)=0
VE^2-VA^2=2gh et h=KL
VE^2=2gKL+VA^2
VE=√(2gKL+VA^2)
Calculons KL
KL=I1B-I1K
Déterminons I1K
On sait qu une circonférence entière est égale 360°
Donc 1/6 de circonférence est égale 360*1/6=60°
Cos 60=I1K/I1A
I1K=I1A*cos60
l1K=Rcos60
KL=I1B-I1K
KL=R-Rcos60
KL=R(1-cos60)
VE=√(2gR(1-cos60)+VA^2)
VE=√2*10*15(1-cos60)+36
VE=√150
VE=12,2 m/s
OK
ELI1 est un triangle rectangle en I1
cos PI/6=I1L/I1E
I1L=I1E*cosPi/6
I1L=R*cosPi/6
AKL1 est un triangle rectangle
CosPi/3=I1K/AI1
I1K=AI1*cosPi/3
I1K=R*cosPi/3
KL=Rcos pi/6-R cos pi/3
KL=R(CosPi/6-CosPi/3)
Non.
Lire l'énoncé et tenir compte des données qu'il fournit :
"le jouet est propulsé en A par un dispositif de lancement , vers le bas , avec une vitesse initiale VA=6 m/s"
Oui.
Sauf si l'énoncé précise la valeur de " g " on convient généralement d'utiliser g = 9,8 m/s²
J'ai trouvé, en gardant 3 chiffres significatifs, VE = 12,0 m/s
Question 3
Appliquons le théorème du centre d inertie
P+N=ma
Projection dans le repéré de frenet
P(Pn=-psin Pi/6, pz=-Pcospi/6), N(Nn=N, NZ=0)= ma(an=VE^2/r,aZ=DV/DT)
On a
-psinPI/6+N=m*VE^2/r
N=Psin pi/6-mVE^2/r
Voici mon travail
Ton résultat est faux
Je ne lis plus tes calculs : Je n'y comprends rien.
J'ai trouvé :
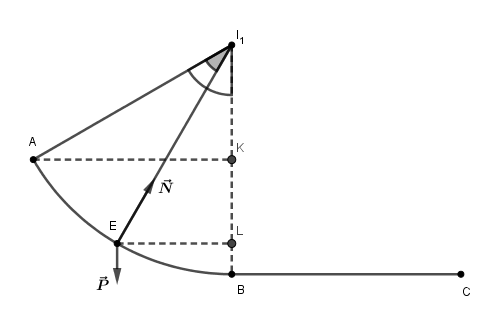
Projection : N - P*cos(α) = m*an
avec :
P = m*g
α = angle (E, I1 , B) ( Voir mon schéma)
an = (VE)² / R
Ce qui donne : N = m * g * cos(α) + m *( (VE)² / R) = m (g * cos(α) + (VE)² / R )
Les valeurs de m, g, α, VE et R sont connues. Il ne reste plus qu'à faire le calcul.
Calculons VB
Appliquons le Théorème de l énergie cinétique
1/2 mVB^2-1/mVC^2=W(P)+W(N) avec W(N)=0
1/2 mVB^2-1/2mVA^2=m g h
Avec h=I1B-I1A'
1/2m(VB^2-VA^2)=mgh
VB^2-VA^2=2gh
VB=√(2gh+VA^2)
h=R-Rcosa or a=0 en B
h=R(1-cosa)
VB=√(2gR(1-cosa)+VA^2)
VB=√(2*9,8*15(1-cos0)+36
VB=√36
VB=6 m/s
Impossible !
Tu trouves que la vitesse de l'objet en B (6m/s) est la même que celle qu'il avait en A (6m/s aussi) !
C'est évidemment impossible.
Et comme, cette fois ci, tu as écrit tes calculs de manière lisible, j'ai pu localiser la cause de ton erreur.
Elle provient du calcul de " h " qui est à revoir à partir de la relation h = I1K = I1B - I1K ( voir ma figure )
Bonsoir
VB=√(2gR(1-cos60)+VA^2)
VB=√2*9,8*15*0,5+36
VB=√183
VB=13,5 m/s
Comme VB>VC donc les forces de frottements existent sur le trajet AC
Oui, c'est exact.
Remarque : Compte tenu de la précision des données ( un seul chiffre significatif pour " m " et pour "VA" ) ce résultat peut être arrondi à f = 0,9N
Si pour une raison quelconque, tu préfères garder 2 chiffres significatifs, le résultat sera de f = 0,89N
La différence entre 0,87N et 0,89N s'explique par une propagation d'erreurs d'arrondis.


