Inscription / Connexion Nouveau Sujet
Bobine
bonjour, j'aurais vraiment besoin pour cet exo, merci.
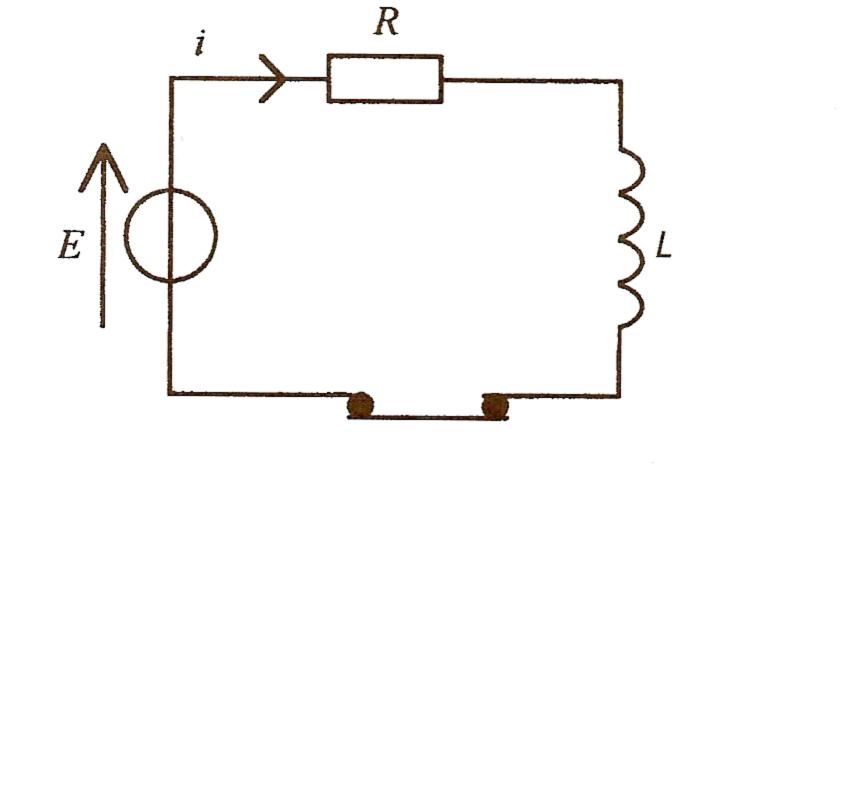
Dans un circuit série constitué d'un générateur de tension continue de f.é.m E, d'une bobine d'inductance L et d'une résistance R, on a enregistré l'évolution de l'intensité du courant i en fonction du temps (i en A; t en s).
1) Établir l'équation différentielle donnant l'intensité du courant i(t) en fonction des données.
2) La solution de cette équation différentielle s'écrit : i = Ke^(-t/(L/R)) + B .
a) Lorsque t tend vers l'infini, l'intensité i(t) est constante ; exprimer cette intensité en fonction de E et R.
b) Exprimer l'intensité i(t) solution de l'équation différentielle sachant qu'à t=0, l'interrupteur est ouvert.
3) Rechercher sur le graphique quelle est la valeur de l'intensité du courant en régime permanent.
4) Exprimer et déterminer graphiquement la constante de temps du circuit.
5) On donne R = 47 Ω.
Déterminer la valeur de l'inductance L et la f.é.m E du générateur.
6) On remplace la résistance de 47Ω par une résistance de 94Ω.
L'enregistrement obtenu est alors le suivant.
1) loi des mailles: UR+UL-E=0 ?
1)
E = Ri + Ldi/dt
di/dt + (R/L).i = E/L
-----
2a)
lim(t-->+oo) i(t) = E/R
---
2b)
i(0) = 0
i = Ke^(-t/(L/R)) + B
0 = K + B --> K = -B
i(t) = B(1 - e^(-t/(L/R)))
lim(t-->+oo) i(t) = E/R
E/R = B(1 - 0)
B = E/R
i(t) = (E/R).(1 - e^(-t/(L/R)))
-----
3)
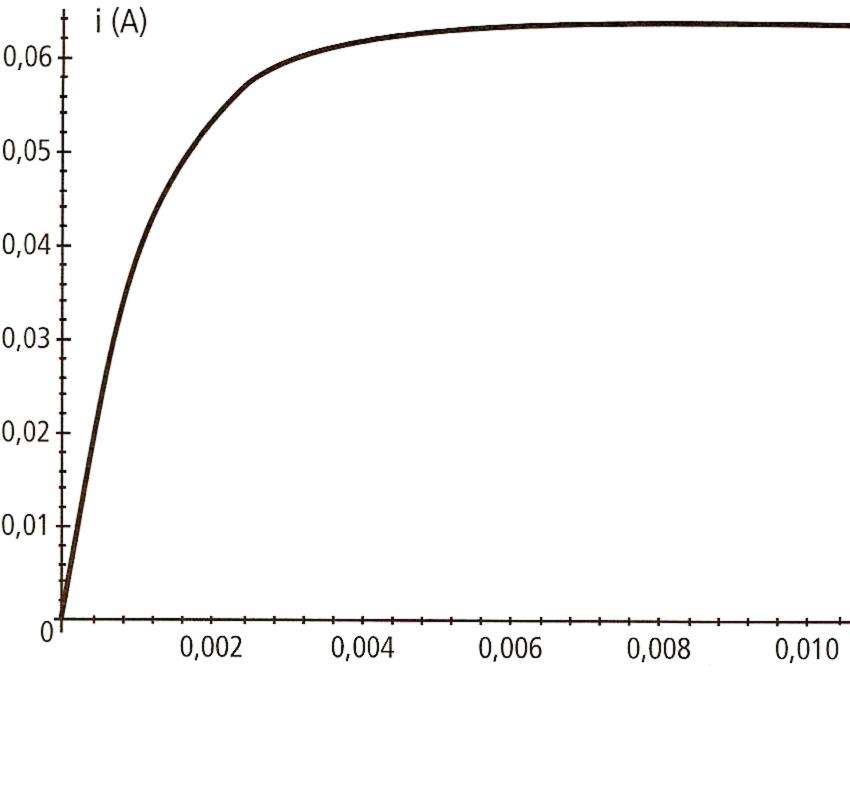
Courant en régime permanent : I = 0,126 A
-----
4)
tau = L/R = 0,0022 s (mesuré sur le graphe)
-----
5)
L/R = 0,0022
L/47 = 0,0022
L = 0,10 H
-----
Recopier sans comprendre est inutile.
Sauf distraction. 
bonjour J-P,
4) je trouve la même valeur que toi pour 
mais sur un autre post que je viens de voir, =0,0013 s ou encore =0,0012 s. donc, comment je peux faire pour trouver la valeur de d'après un calcul ?
On apprend à l'école qu'on trouve la constante de temps en traçant la tangente à la courbe à l'origine et ...
(Comme le tracé en mauve).
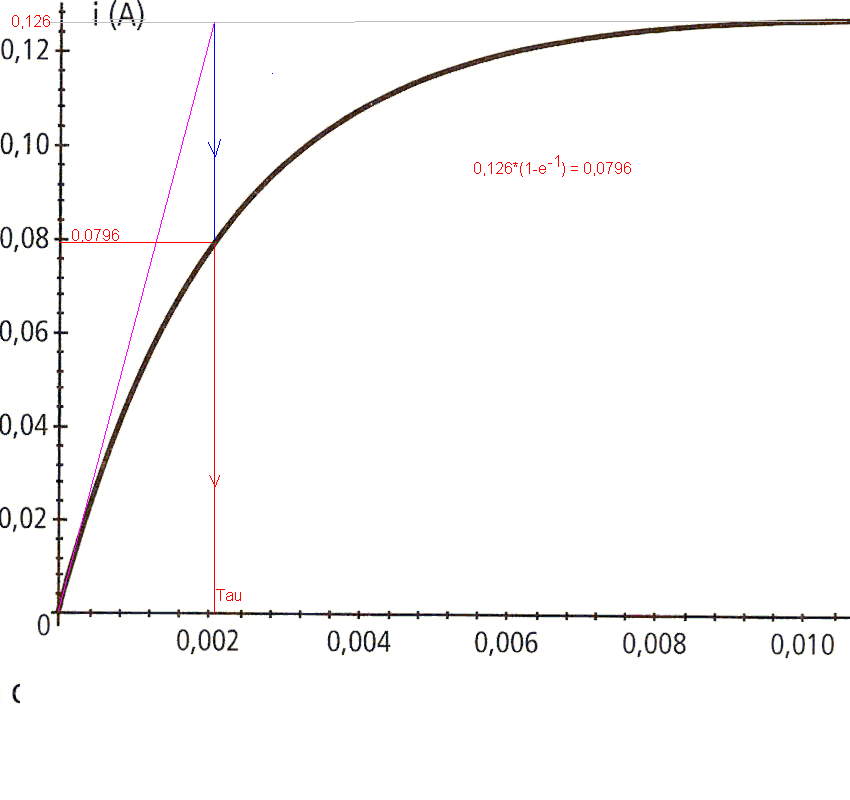
Ceci est mathématiquement correct mais ...
Il est très difficile de tracer avec précison la tangente et donc cela entraîne une grande imprécision sur l'évaluation de la valeur de Tau.
Il y a une autre manière, bien plus plus précise pour trouver Tau.
Dans le cas d'un signal d'expression : i(t) = Imax.(1-e^(-t/tau)), on calcule la valeur de i pour t = 1 * tau, on trouve :
i(tau) = Imax * (1 - e^-1) = Imax.(1 - 0,3679) = 0,6321 Imax (arrondi)
On trace donc une // à l'axe des abscisses à une ordonnée valant 0,6321.Imax (ici, cela vaut 0,126 * 0,63 = 0,796) et on trouve Tau comme indiqué (en rouge) sur le dessin.
La construction par cette méthode est plus facile à réaliser avec précision et donc la valeur de tau trouvée est plus précise ainsi.
Sauf distraction.
Annuler
connectez vous