Inscription / Connexion Nouveau Sujet
auto induction
Bonsoir
Énoncé:
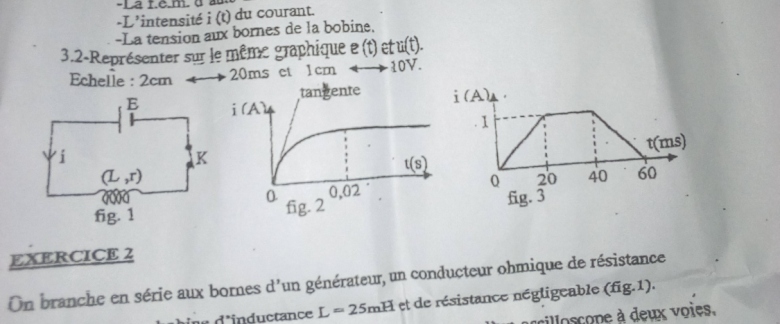
Un circuit en série se compose d un générateur de f.e.m E=25 V et de résistance interne négligeable , d un interrupteur et d une bobine d inductance L et de résistance r (fi 1). On ferme l interrupteur a l instant t=0 s .on enregistré les variations de l intensité l du courant en fonction du temps (figure2)
Le coefficient directeur de la tangente a l origine est 50 SI
Au bout de t=0,02 s,on peut considérer que le courant est établi,son intensité étant constante et égale a 1 A.
1/ exprimer la f.e.m d auto induction en fonction de E,r et i
2/déduire de la courbe (fig2) les valeurs de r et L.
3/le générateur délivré maintenant un courant dont l intensité est représente sur la figure 3.
3/1 déterminer dans chaque phase :
La f.e.m d auto induction e.
L intensité i(t) du courant.
La tension aux bornes de la bobine.
3/2 représenter sur le même graphique e(t) et u(t)
Échelle :
2 cm==> 20 ms et 1 cm==> 10 V
Réponse
Question 1
e=-L*di/dt
Mais je n ai pas trouvé E ,r et i dans l expression
Bonsoir
En appliquant la loi daddition des tensions ou la loi des mailles. Tu va obtenir une relation entre di/dt, R, R et i. Il te suffit d'étudier 2 cas: l'instant initial et la limite du courant continu.
La loi d addition
UE : désigné la tension au bornes du générateur
U;la tension au borne de la bobine.
Selon moi
UE=U
Est ce que c est correct
D'où l'équation :
E=R.i+L.di/dt
A appliquer à l'instant initial pour obtenir L puis à appliquer au régime continu pour obtenir r.
Attention aux notations ! désigne la dérivée de i par rapport à t, pas un rapport de deux grandeurs ! Soit f la fonction telle que i=f(t), les mathématiciens noteraient f'(t) cette dérivée plutôt que
!
Revois bien ton cours de math sur la notion de dérivée et son lien avec le coefficient directeur de la tangente à la courbe représentative. Observe bien la courbe représentant les variations de i en fonction de t. "Comme par hasard", la tangente à la courbe est tracée au point d'abscisse t=0. Puisque l'échelle est fournie, tu peux déterminer graphiquement le coefficient directeur de cette tangente. Puisque i=0 pour t=0, à cet instant initial :
; tu pourras ainsi obtenir L.
OK
Il te reste maintenant à étudier le régime continu : i=constante=ordonnée de l'asymptote horizontale à la courbe i=f(t). Alors : , donc : ...
Raisonnement correct mais attention : une application numérique non accompagnée de son unité correcte, lorsqu'elle existe évidemment, est considérée comme fausse dans la plupart des examens et concours...
Il te faut calculer dans les trois cas :
* t<20ms
* 20ms<t<40ms
* 40ms<t<60ms.
Restera ensuite à appliquer les formules générales :
Tu as (encore...) oublié l'unité mais le calcul du coefficient directeur est correct.
Attention : tu as tout intérêt à exprimer t en seconde et non en millisecondes.
Le coefficient directeur s'obtient en soustrayant la valeur initiale à la valeur finale.
Au numérateur : 0-1 et non 1-0.
Tu as tout de même suivi des cours de mathématiques. Cas 3 : le coefficient directeur est négatif comme déjà dit.
J'avais compris, bien sûr, que c'était une étourderie et pu ainsi constater que je n'étais pas le seul à en avoir.
J'ai préféré tout de même le signaler de crainte que moussolony ne s'en rende pas compte.
Bonjour odbugt1
J'ai préféré tout de même le signaler de crainte que moussolony ne s'en rende pas compte.
Crainte tout à fait justifiée... En tous cas : merci pour la correction !

Bonjourmoussolony
Il me semble t'avoir déjà rappelé la définition du coefficient directeur d'une droite :
en posant : t2=60ms et t1=40ms
Je ne suis pas sûr que tu ais bien compris en cours de math la signification du signe d'une dérivée ; puisque, dans le cas 3, l'intensité décroit en fonction du temps, la dérivée ne peut qu'être négative ...
Les questions précédentes ont permis d'obtenir les valeurs de L et r. Tu n'as plus qu'à faire les trois applications numériques.
Relis bien l'énoncé : il s'agit d'obtenir u(t) soit l'expression de u en fonction de t.
Sur le premier intervalle de temps, est constant mais i est une fonction du temps. Il te faut donc commencer par obtenir i(t) entre 0 et 20ms avant d'appliquer la formule générale :
.
Si je peux me permettre un conseil : je pense que tu te disperses trop en menant en même temps de nombreux exercices, souvent sur le même thème. Tu finis par ne plus avoir en tête les énoncés précis puisque la recherche d'un même exercice s'étale parfois sur plusieurs semaines.
La question ici est d'obtenir u sachant que r et i sont connues.
Tu fais exactement la même erreur que celle commise pour le cas 1 dans ton message du 11-03-20 à 13:38. La réponse fournie alors reste donc valide : il te faut exprimer i en fonction de t avant d'utiliser la formule
Entre t=40ms et t=60ms, la courbe représentant les variations de i en fonction de t est une droite. Il est donc possible d'écrire son équation sous la forme :
i=a.t+b
en écrivant : i=1A si t=4.10-2s
et : i=0 si t=6.10-2s,
tu obtiens un système de deux équations permettant d'obtenir les valeurs de a et b.



