Niveau terminale

Applications dynamiques

Posté par
beugg 08-02-17 à 19:02

Bonjour mes amis
Pourriez m'aider sur l'essentiel du cours : "Applications dynamiques"

J'aimerais juste savoir ce qu'on doit en retenir

J'ai un cours mais c'est un peu désordonnée quoi ...

Merci de vouloir bien m'aider

Posté par re : Applications dynamiques 08-02-17 à 19:14

Salut beugg.

Commence par regarder les fiches disponibles sur le site [lien]
Thème 2, partie 1 : Temps, mouvement et évolution.

Tu y trouveras des exemples de situations et d'exercices qu'il faut savoir refaire.

Bon courage.

Posté par re : Applications dynamiques 08-02-17 à 19:30

Merci picard pour cette réponse rapide.

Je vais suivre votre conseil ,OK à plus

Posté par re : Applications dynamiques 08-02-17 à 20:01

A plus !

Posté par re : Applications dynamiques 21-02-17 à 20:05

Bonsoir picard

Au niveau de "mouvement d'un projectile dans le champ de pesanteur " et de "chute libre verticale" , on a des relations d'équations en intégrant .Et moi je n'ai pas encore fait le cours sur l'intégration sauf j'ai pris quelques notions d'intégration nécessaires .

Ici je n'ai pas bien compris la façon à laquelle on a intégré.

Merci de m'expliquer

Posté par re : Applications dynamiques 22-02-17 à 16:22

Bonjour beugg.

Citation :
je n'ai pas encore fait le cours sur l'intégration

Le problème n'est pas nouveau, il n'y a jamais eu d'entente entre les profs de maths et de physique ni sur un calendrier ni sur le vocabulaire...

Si tu as réussi à acquérir quelques notions sur l'intégration ça devrait pouvoir s'arranger.

Dans le cadre d'un cours de terminale S, tu n'auras en général à intégrer que dans quelques situations (mouvements de projectiles, mouvements d'oscillateurs, décroissance radioactive, circuits RL, RC ou RLC série).

On va se limiter ici au seul cas des mouvements de projectiles.

Tu dois au préalable mémoriser l'expression des dérivées des fonctions polynômes...

fonction	dérivée
y = a	y' = 0
y = ax + b	y' = a
y = ax² + bx + c	y' = 2ax + b

Comme l'intégration est l'opération qui consiste à retrouver une fonction quand on connait la dérivée, mémorise aussi l'expression des primitives des fonctions polynômes.

fonction	primitive
y = 0	Y = a
y = a	Y = ax + b
y = ax + b	Y = 1/2 ax² + bx + c

Après ces préambules, regardons la suite sur un exemple.

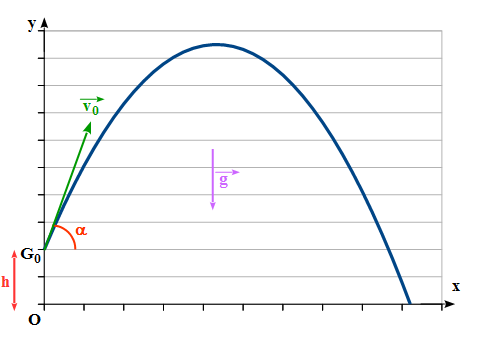
Un projectile de masse m, est lancé à l'instant t = 0, dans un champ de pesanteur uniforme $\vec{g}$ depuis un point G₀, avec une vitesse initiale $\vec{v_0}$ , faisant avec l'horizontale un angle $\alpha$ .
La position du projectile est repérée dans le repère (xOy) (cf schéma).

On veut déterminer l'équation de la trajectoire du projectile dans le repère.

Il est intéressant de récapituler, pour commencer, les conditions initiales du mouvement (càd, la position et la vitesse du projectile à t = 0).

-Position initiale : G₀ (x₀ = 0 ; y₀ = h)
-Vitesse initiale : $\vec{v_0}$       coordonnées dans le repère : $v_{0 x} = v_0 cos  \alpha$      et     $v_{0 y} = v_0 sin  \alpha$

L'application de la seconde loi de Newton permet d'établir que l'accélération du projectile est : $\vec{a} = \vec{g}$
Je passe très vite là dessus, c'est du classique et il n'y a pas de grosses difficultés à surmonter.

Coordonnées de l'accélération : comme $\vec{a} = \vec{g}$ , on a : $a_x = 0$ (car $\vec{g}$ est perpendiculaire à Ox)     et     $a_y = -g$ (car $\vec{g}$ est de même direction et de sens contraire que Oy , d'ou le signe -).

Coordonnées de la vitesse : par définition, $\vec{a} = \dfrac{d\vec{v}}{dt}$
Pour avoir $\vec{v}$ , il faut donc intégrer $\vec{a}$ .
Ici, la variable de dérivation est le temps t et non x, comme en maths...

En fait, on est amené à chercher les primitives des coordonnées de $\vec{a}$ pour trouver celles de $\vec{v}$ .

Détermination de $v_x$

Comme $a_x = 0$ ,     $v_x$ sera une constante (regarde ton tableau fonction/primitive).

On va écrire, pour commencer : $v_x = K_1$      $K_1$ désignant une constante (d'intégration).

Pour déterminer cette constante $K_1$ , il faut prendre en compte les conditions initiales...

On a écrit que à t = 0, on avait : $v_{0 x} = v_0 cos  \alpha$

Cela doit être vérifié aussi à tout instant...On aura donc :   $v_x = K_1 = v_0 cos  \alpha$

Et donc, finalement :   $v_x = v_0 cos  \alpha$

Détermination de $v_y$

Comme $a_y = -g$ ,     $v_y$ sera une fonction affine du temps (cf tableau fonction/primitive).

On va écrire, pour commencer :   $v_y = -g t + K_2$        ( $K_2$ constante d'intégration)

Détermination de $K_2$ par prise en compte des conditions initiales.

A t = 0, on a vu plus haut que :     $v_{0 y} = v_0 sin  \alpha$

Or, à tout instant on a aussi : $v_y = -g t + K_2$
en faisant t = 0, dans cette expression, on a : $v_y = -g \times 0 + K_2 = v_{0 y} = v_0 sin  \alpha$
soit encore : $0 + K_2 = v_{0 y} = v_0 sin  \alpha$

Et donc : $K_2 = v_{0 y} = v_0 sin  \alpha$

Finalement, on aura donc :     $v_y = -g t + v_0 sin  \alpha$

Coordonnées du vecteur position: par définition,     $\vec{v} = \dfrac{d \vec{OG}}{dt}$
Pour avoir $\vec{OG}$ il faut donc intégrer $\vec{v}$

Détermination de l'abscisse $x$ de G

Comme $v_x = v_0 cos \alpha$    $x$ va être fonction affine du temps

On a, tout d'abord : $x = v_0 t cos \alpha + K_3$      ( $K_3$ constante d'intégration)

Prise en compte des conditions initiales pour trouver $K_3$

A t= 0, $x_0 = 0$     donc     $x = v_0 \times 0  cos \alpha + K_3 = 0$      soit     $K_3 = 0$

Finalement, on a donc :     $x = v_0 t cos \alpha$

Détermination de l'ordonnée $y$ de G

Comme $v_y = -g t + v_0 sin \alpha$      $y$ va être du second degré par rapport à t.

On a tout d'abord : $y = -\dfrac{1}{2} g t^2 + v_0 t sin \alpha + K_4$      ( $K_4$ constante d'intégration)

Prise en compte des conditions initiales pour trouver $K_4$

A t = 0, $y_0 = h$      donc     $y = -\dfrac{1}{2} g \times 0^2 + v_0 \times 0 \times sin \alpha + K_4 = h$
Ce qui conduit à $K_4 = h$

Et donc, finalement : $y = -\dfrac{1}{2} g t^2 + v_0 t sin \alpha + h$

Pour obtenir l'équation de la trajectoire du projectile, on part de l'expression de l'abscisse :
$x = v_0 t cos \alpha$      d'où on tire   $t = \dfrac{x}{v_0 cos \alpha}$

En remplaçant $t$ par cette valeur dans l'expression de $y$ , on obtient :
$y = -\dfrac{1}{2} g {\dfrac{x}{v_0 cos \alpha}}^2 + v_0 \dfrac{x}{v_0 cos \alpha} sin \alpha + h$

Ce qui, après simplification conduit à :       $y = -{\dfrac{g}{2 {v_0}^2 cos^2 \alpha}} x^2 +x  tan \alpha + h$

J'ai passé pas mal de temps à écrire tout ça, j'espère n'avoir pas fait d'erreur ; si jamais quelque chose te paraît suspect, dis le moi.

A plus et bonne lecture.

Applications dynamiques

Posté par re : Applications dynamiques 23-02-17 à 21:12

Vraiment c'est impeccable M Picard

Merci beaucoup encore une fois

À très bientôt

Posté par re : Applications dynamiques 24-02-17 à 08:13

Si cela t'a aidé, c'est parfait !

Bon courage et à plus.

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de physique

Fiches de niveau terminale
41 fiches de physique - chimie en terminale disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Applications dynamiques

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de physique