Inscription / Connexion Nouveau Sujet
Applications des bases de la dynamique
PENDULE CÔNIQUE
Bonsoir,excusez du dérangement mais je voulais juste poser une tout petit question concernant la question 1) de cette exercice
Exercice
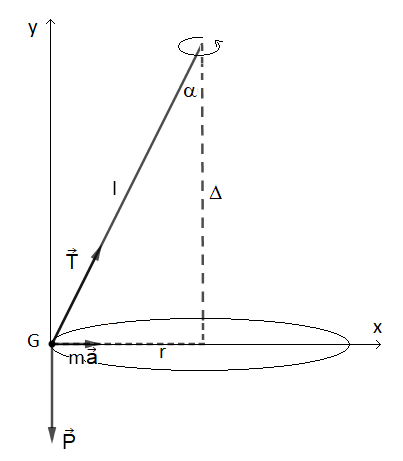
Un solide métallique de masse m=20g est suspendu à l'extrémité d'un fil inextensible de longueur l=50cm,l'autre extrémité est fixée en un point si d'un axe verticale .Lorsque cet axe à une vitesse angulaire suffisante,Le fil s'incline d-un angle
par rapport à la vrrtcverticale et le centre d'inertie G du solide décrit un mouvement circulaire uniforme autour de l'axe
1)En appliquant le principe fondamental de la dynamique ,montrer que la vitesse angulairewangulaire de rotation du solide est constante et l'exprimer en fonction de l,g et
2)Quelle valeur minimale peut prendre cette valeur sera noté wmin
Ma question consterné la 2)
Pourquoi si on projette suivant le vecteur poids,on ne trouve pas
la même valeur que wmin
Bonjour,
Ma question consterné la 2)
Pourquoi si on projette suivant le vecteur poids,on ne trouve pas
la même valeur que wmin
" Consterné " moi aussi de ne pas comprendre ta question.
Il faut projeter la 2ème loi de Newton sur les deux directions pour obtenir l'expression de la vitesse angulaire et en déduire sa valeur minimale.
Projection suivant l'axe du vecteur un
Vecteur P+vecteur Y=m×vecteur an
On obtient
T=mw2l (1)
Projection suivant le vecteur P
P-Tcos =0
T=(mg)/(cos)
Ma question est pourquoi pourquoi si je projette suivant le vecteur T je ne trouve pas le même résultat que suivant vecteur P
Voici ce que je trouve suivant vecteur T
T-Pcos=0
T=Pcos
Normalement ne devons t-on pas trouver la même chose
Je ne vois pas trop l'intérêt de projeter la 2e loi de Newton selon la direction du fil puisque les projections "classiques" suivant un rayon du cercle et un axe perpendiculaire à ce rayon suffisent à résoudre le problème.
Mais ..... admettons
Ta relation T - m g cos() = 0 est fausse car la projection du vecteur accélération sur la direction du fil n'est pas nulle.
Pourtant je n'est fait qu'appliquer la condition d'equilibre (somme des forces extérieur est un vecteur nulle)
L'accélération n'est pas une force
L'énoncé indique :
le centre d'inertie G du solide décrit un mouvement circulaire uniforme autour de l'axe \Delta }
Dans un référentiel terrestre le centre d'inertie G du solide n'est pas en équilibre et il est donc faux d'écrire que la somme vectorielle des forces extérieures est nulle.
En revanche, tu peux appliquer le 2e loi de Newton :
et utiliser le fait que puisque le mouvement de G est circulaire et uniforme le vecteur accélération est centripète et de module ||a|| = v²/r =
²r=² l sin()Cette relation ne suffit pas pour trouver la valeur de w(T=mw2l)
Donc il faut que j'obtienne une autre relation avec la tension pour pouvoir calculer w
Bien d'accord !
On en revient donc à ce que j'écrivais dès 9h37 :
"Il faut projeter la 2ème loi de Newton sur deux directions"
On va donc projeter :
sur Ox et Oy
Oui j'ai déjà fait ça
Regardez mon message précédent (on trouve T=w2×m×l)
Pour calculer w il faut que j'élémine T de mon expression.Donc j'ai besoin d'une autre relation incluant T pour pouvoir ensuite égaliser les deux résultats (T=T )(c'est ainsi que T disparaîtra de l'expression que je veux obtenir de w)
Avez vous compris ce que je veux dire?
Mais oui, j'ai compris !
Donc sur l'axe Ox :
0 + T sin(α) = m ω² l sin(α)
soit T = m ω² l
Tu as déjà fait ça ! (Aujourd'hui à 09h44)
Et maintenant sur l'axe Oy :
- mg + T cos(α) = 0
soit T = mg / cos(α)
Tu as déjà fait ça aussi ! (même jour, même heure)
On égale les deux valeurs de T :
m ω² l = mg / cos(α)
ω² = g/ l cos(α)
ça tu ne l'avais pas fait !
Et on obtient ce qu'on cherche :
En revanche ce que j'ai moins compris :
Pourquoi avoir voulu projeter sur la direction du fil ? (Toujours même jour même heure)
Pourquoi avoir voulu que le système soit en équilibre ? (Même jour, mais un peu plus tard 12h22)
J'ai voulu refaire l'exercice en choisissant cette fois ci pour axe des ordonnée la direction suivant vecteur T
Mais aprés j'ai qu'elle était mon erreur
L'axe des ordonnées doit toujours être perpendiculaire à celle des abscisses.Ce qui n'est pas le cas si je choisis la direction suivant un comme abscisse et la directionsuivant T comme ordonnée
Donc en Clair,depuis le début mes projections étaient fausses
Merci j'ai compris
Également une dernière question,quand appliqu'on la condition d'équilibre de deux forces non parallèles
J'ai voulu refaire l'exercice en choisissant cette fois ci pour axe des ordonnée la direction suivant vecteur T
Mais aprés j'ai vu quelle était mon erreur
L'axe des ordonnées doit toujours être perpendiculaire à celle des abscisses.Ce qui n'est pas le cas si je choisis la direction suivant vecteur un comme abscisse et la direction suivant T comme ordonnée
Donc en clair,depuis le début mes projections étaient fausses
Merci j'ai compris 😀😀😀😀
Également une dernière question,quand appliqu'on la condition d'équilibre de deux forces non parallèles
Tu peux projeter les relations vectorielles sur les axes de ton choix et il n'est pas absolument indispensable que ces axes soient perpendiculaires.
Le choix des axes est important.
Ils seront choisis de manière à obtenir les équations les plus simples possibles et c'est vrai que dans l'immense majorité des cas on a intérêt à choisir des axes perpendiculaires.
Je n'ai pas compris ta "dernière question"
Annuler
connectez vous