Bonjour,
J'ai besoin de votre aide pour résoudre ce problème de physique :

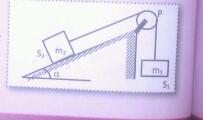
''Deux solides S1 et S2 de masses respectives m1 et m2 dont reliés par une corde inextensible de masse négligeable passant par la gorge d'une poulie (P) de rayon R tournant autour d'un axe (Delta) confondu avec l'axe de rotation de la poulie. Le moment d'inertie de la poulie par rapport à cet axe est J(Delta). Le solide S2 grimpe sans frottement sur un plan incliné d'un angle alpha. La position de S2 est repérée sur un axe (Ox) par l'abscisse x de son centre d'inertie. A l'instant initial, le solide S2 est à l'origine de l'axe (Ox). Un dispositif informatique approprié permet de relever les abscisses, de calculer les vitesses instantanées et de tracer le graphe ci-contre. Données: m1=400g ; m2=300g; g=10m/s²; R=10cm ; J(delta)=0,0055 kg/m².

1.'exploitation de la courbe. À partir du graphe V=f(t), déterminer :
1-1) La nature du mouvement du solide.justifier votre réponse.
1-2) la valeur expérimentale de l'accélération linéaire a(exp) du solide S2.
1-3) La loi horaire du mouvement de S2.
2-Étude théorique
2-1) Appliquer le TCI au solide S1 et donner l'expression de l'accélération linéaire théorique a(th) en fonction de m1, g et T1 (intensité de la tension du fil).
2-2) Appliquer le TCI au solide S2 et donner l'expression de l'accélération linéaire théorique a(th) en fonction de m2, g et T2 (intensité de la tension du fil) .
2-3) Appliquer la RFD à la poulie en rotation et donner l'l'expression de l'accélération angulaire de la poulie en fonction de T1, T2, R et J(delta).
2.4) À partir des questions précédentes, montrer que l'l'expression de l'accélération linéaire des deux masses peut se mettre sous la forme .
3-synthèse
3-1) Quelle hypothèse de l'énoncé permet de considerer que a(th)=a(exp) ?
3-2) En déduire l'angle alpha de plan incliné.


Ma proposition :
1-1) le mouvement est rectiligne uniformement accéléré ; car sa trajectoire est une droite et sa vitesse croit au cours du temps.
1-2) a(exp)=delta-V/delta-t
a(exp)=(Vf-Vi)/(tf-ti)=(0,5-0,28)/(0,065-0)≈3,4 m/s².
1-3) D'après le cours, pour avoir cette loi horaire, on intègre a(exp) deux fois en fonction de t.
Vu qu'au début le solide était à l'origine du repère, x(t)=0 à t=0.
Je trouve par "tâtonnements" x(t)≈1,7t² : bien qu'on a pas encore passé les cours sur les intégrales.

2-1) Application du TCI au système S1:
Système étudié : masse suspendue par un fil.
Référentiel terrestre supposé galiléen ;
Inventaire des forces appliquées:
Poids P1; Tension T1.
D'après le TCI, P1+T1=m1a(th)
Suivant le sens de mouvement on a en module:
P1-T1=m1a(th)
=> a(th)=(m1g-T1)/m1

2-2) D'après le TCI,
En vecteur on a:  P2+T2=m2a(th)
Suivant le sens de mouvement (x'x) on a en module:
-P1sin(alpha)+T2=m2a(th) =>
a(th)=(T2-m2gsin(alpha))/m2
2-3) La poulie est en rotation: la somme des moments des forces extérieures appliquées est égal au produit de J(delta) et l'accélération angulaire (a(ang)).
Les forces appliquées à la poulie sont T1 et T2:
T1R-T2R=J(delta)a(ang)
=> a(ang)=(T1R-T2R)/J.delta

2.4) Mais ici,  je ne sais pas comment ressortir une relation entre les deux premières accélérerations qui se valent et la dernière pour avoir une acceleration des deux masses en fonction de R et J-delta.