Inscription / Connexion Nouveau Sujet
Alignement Terre Mars
Bonjour,
Pouvez-vous m'aider pour cet exercice ?
On suppose les orbites de la Terre et de Mars circulaires, de rayon respectifs 1 et 1.5, et coplanaires, décrites respectivement en un temps Tt et Tm.
A l'instant initial, les deux planètes sont alignées. Donner le temps, en année, qui s'écoulera avant un nouvel alignement (littéralement puis faire l'A.N.).
Dans les deux cas, l'orbite étant supposée circulaire, on assimile le demi grand axe au rayon. On note r1 et r2 les rayons respectifs de la Terre et de Mars.
On note m1, m2 et M les masses respectives de la Terre, de Mars et du Soleil. On a M >> m1 et M >> m2.
D'après la 3ème loi de Kepler, en prenant comme unités, la masse solaire, l'U.A. et l'année :
r1³/Tt² = GM/(2pi)² = 1 = GM/(2pi)² = r2³/Tm²
D'où r2³/Tm² = r1³/Tt² <=> Tm= (3/2)Tt
J'ai une idée de la réponse (1.5 ans) , mais je ne vois pas trop comment procéder.
Merci par avance !
Bonsoir
Tout est ok sauf la dernière égalité et ton intuition est fausse. Fais apparaître l'égalité entre le rapport des carrés des périodes et le rapport des cubes des rayons puis écris l'égalité des racines carrées des deux termes...
Merci beaucoup vanoise.
Ah oui effectivement, erreur de calcul 
. Je reprends :
C'est là que je coince, je ne vois pas comment utiliser ce résultat.
Pour plus de clarté il faut harmoniser les notations. Si pour les périodes, on utilise les indices t et m, il faut faire de même pour les rayons de trajectoires. Ainsi :
Soit, la période étant mesurée en année sidérale terrestre :
D'accord, merci.
1,8 années correspond à la période de rotation complète de la planète Mars, si je ne me trompe pas.
Comment peut-on faire pour en déduire le temps qui s'écoulera avant un nouvel alignement ?
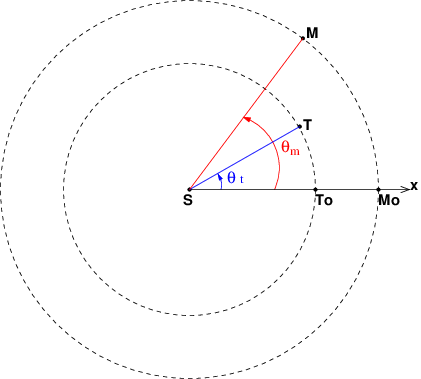
Le schéma ci-dessous devrait t'aider.Je choisis un axe de référence (Sx) où S est le centre du soleil de sorte que les centres To et Mo de la terre et de mars appartiennent à cet axe à la date t= 0 d'un alignement. Cet axe est fixe dans le repère de Copernic. A une date t quelconque ultérieure, la terre a tourné de l'angle 
t = 
t.t tandis que mars a tourné de l'angle m=m.t
t représente la vitesse angulaire de rotation de la terre ; quelle est la relation simple entre t et Tt l'année sidérale de la terre ? De même, quelle est la relation entre m et Tm ?
Maintenant : quelle est la plus petite valeur de (m - t) pour qu'il y ait à nouveau alignement ?
Je te laisse réfléchir...
Merci vanoise pour ces indications très utiles !
On a : et
. Les planètes seront de nouveau alignées lorsque
; si l'on suppose que ceci arrivera en un temps
, on obtient :
Après application numérique, si je ne me trompe pas, on trouve 1 an 35 jours et 13 heures.
Ton énoncé manque de précision car il existe deux sortes d'alignements :
1° : celui que tu considères en posant t - m = 
.Il s'agit bien d'un alignement au sens mathématique du terme mais en général, les astronomes ne prennent pas en compte ce type d'alignement car la terre et mars sont de part et d'autre du soleil ; mars n'est pas visible de la terre dans ces conditions.
2° : pour la raison précédente, on s'intéresse essentiellement aux alignements tels que les planètes sont du même côté du soleil, comme sur la figure que j'ai fournie précédemment. La durée entre deux alignements de même nature est le double de la valeur précédente car elle correspond à :
t - m = 2.
La durée t2 entre deux alignements de même nature vérifie :
Impossible de savoir ici de quel type d'alignement parle l'énoncé.
Attention à la précision des résultats. l'astronomie est une science très précise et les données sont disponibles sur le net avec une très grande précision. Cependant ici, l'énoncé ne fournit que deux chiffres significatifs. Il faut donc fournir le résultat avec également deux chiffres significatifs. Il aurait fallu arrondir ton calcul à 1,1année, le calcul que je t'ai présenté conduisant à 2,2années (années sidérales terrestres).
Annuler
connectez vous
en post-bac