Bonjour Estelle, tu as changé de centre d'intérêt, depuis... deux ans !...

    Je ne suis pas du tout spécialiste, mais je dirais qu'une bouteille en verre ( couchée, et bouchée (?) ), est (presque) aussi bien profilée qu'un avion moderne (sans les ailes ! ) , me semble-t-il ...
    Quant à sa  surface de référence , ce doit être sa section  (perpendiculaire au mouvement )

Bonjour jacqlouis

Pas vraiment... mais c'est un projet obligatoire, une épreuve du bac !

Il s'agit d'une bouteille d'eau en plastique, de 50 cL, pleine ou vide telle est la question, et verticale.

Estelle

Si la bouteille est verticale (posée "debout" comme on la pose normalement...) elle n'a pas un profil vraiment aérodynamique, non... ?

Merci

Estelle

salut Estelle

toujours sur Wiki pour calculer la force de trainée :



je pense qu'elle est faible cette force de trainée par rapport aux autres  ..

    Un peu quand même, puisque cylindrique .... mais est-ce que cela influe beaucoup, étant donné la faible vitesse des tapis roulants ?...

Salut disdrometre

Je dois y aller mais je regarde à mon retour !

A tous les deux >> A moi aussi elle me paraît faible mais j'ai demandé à mon prof de méca, et il attend que je traite de cette force dans mon projet donc... je la traite.

Merci

Estelle

S est ce qu'on appelle le "maître-couple" en  aérodynamique,

C'est tout simplement l'aire de l'objet qui s'oppose au mouvement dans l'air. Soit l'aire qui est vue par un observateur qui se trouve sur la trajectoire de l'objet.

Dans mon dessin d'une bouteille (pas très jolie), le S est l'aire en bleue, c'est l'aire des 2 rectangles, il ne faut pas calculer l'aire "bombée" réelle de la bouteille.

Merci beaucoup J-P, tu me sauves !

Estelle

Et pour le coefficient Cx... ?

Estelle

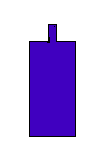
J'avais lu "il ne faut pas oublier de calculer l'aire "bombée" réelle de la bouteille" mais tu dis bien qu'il ne faut PAS la calculer... pourquoi ?

Merci

Estelle

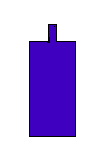
     L'aire à prendre en compte est, bien sûr , la section pêrpendiculaire au mouvement,
    mais ici la forme cylindique diminue le coefficient de traînée (une bouteille de section carrée , pe. Vodka ? , aurait un coeeficient plus grand...

Pour une bouteille cylindrique, il faut en fait prendre la demi-aire ?

Estelle

    Non, pas la demi-aire ...
L'aire vue par le "courant d'air" qui s'oppose au mouvement , c'est bien l'aire de la section (perpendiculaire au mouvement, je me répète), c'est-à-dire , à peu près,  l'aire en rouge sur le dessin plus haut ...
    mais le coefficient de traînée sera plus faible avec ta bouteille cylindrique (arrondie), qu'avec une bouteille "carrée" de même surface "rouge" (cf le dessin).
    Une barque à l'avant plat avance moins vite dans l'eau qu'un kayaak fuselé...  

* Comment une aire peut-être perpendiculaire à une direction ?

* Finalement, pour le coefficient de traînée, Wikipedia me propose deux valeurs suivant que l'objet est ou non d'une forme aérodynamique :

Les CX que tu annonces me semble bien loin de la réalité.

Le Cx dépend du nombre de Reynolds qui lui même dépend de la vitesse du fluide (ici l'air) et de la viscosité dynamique du fluide (ici l'air).

La faible viscosité dynamique de l'air fait qu'on est presque toujours avec un nombre de Reynolds élevé. (mais pas très très élevé à cause de la vitesse relativement faible)

Pour une sphère, on a alors Cx = 0,5 environ.

On est dans le plat de la courbe qu'on peut trouver ici :

Pour une bouteille verticale, je taperais au pif, le CX proche de 1.

A titre d'exemple,

Les voitures bien profilées ont un CX d'environ 0,3
(mieux qu'une sphère).

La vitesse de l'air... comment peut-on la déterminer ?

Pour la viscosité dynamique de l'air, d'après ce tableau : >> , je pense qu'on peut prendre .

Avec ça, je peux déterminer le nombre de Reynolds ? Est-ce que tu pourrais me donner son expression en fonction de la vitesse et de la viscosité dynamique du fluide ?

Et ensuite, comment déterminer le Cx grâce au nombre de Reynolds ?

Si tout cela devient trop compliqué, je me mettrai de prendre une valeur de Cx indicative comme 1...

Merci !

Estelle

Autre question :

Pour justifier l'expression de la force de traînée, il est marqué

La vitesse de l'air par rapport à la bouteille sera la vitesse du tapis roulant.

Nombre de Reynolds :

vitesse du tapis ????  dans [1 ; 10] m/s (à toi de savoir).

L = 0,3 m (pour une bouteille)

Re = 0,3 * V/(18.10^-6) = 16600.v

Donc 16600 < Re < 166000

Si tu vas voir le lien que j'ai donné pour la sphère, on a alors Cx = 0,5 (à rien près) pour toute la gamme de valeur de Re.
-----

Ce sera vrai aussi pour un cylindre (CX quasi constant pour la gamme de Re qui correspond à l'exercice), mais le coefficient de pénétration dans l'air de la bouteille est moins bon que celui d'une sphère.

Et donc le CX constante > 0,5 pour la bouteille dans le cas de l'exercice.

Je n'ai pas de courbe de CX pour le profil de la bouteille, et je donne alors une valeur au pif qui est CX proche de 1.

Ce n'est que du "au pif", mais en général j'ai un assez bon nez.  

D'accord, j'ai bien compris, merci =)

Mais comment ils ont fait pour tracer cette courbe pour la sphère ? Expérimentalement ?

Estelle

Tu peux aller voir les liens à l'intérieur de celui que je t'ai donné.
  
On y parle des phénomènes qui entraînent les non linéatités, mais c'est très loin d'être évident.


  

Ici : >> .

Sur la figure 4, nous sommes dans la situation 1.

Plus bas sur la page, on trouve [url]http://www.univ-brest.fr/lpo/mouillages/visualiser/m02_fichiers/image008.gif[url].
Avec les valeurs que tu as calculé plus haut, on peut dire que Cx ~ 1,... non ? Mais j'ai des problèmes pour comprendre l'échelle des ordonnées... Quoi qu'il en soit, c'est bien ça qu'il faut regarder, non ?

Estelle

L = 0,3 m
C'est à peu près la hauteur de la bouteille.

Il faut prendre une dimension "honnète", qui est dans les dimensions de la bouteille, tu peux prendre 0,1 m si tu veux, peu importe.

C'est juste une mesure qui "ressemble" à une mesure de la bouteille et qui permet juste de voir où on en est pour le nombre de Reynolds.

On ne peut pas prendre 1 mm, ou 2 m par exemple, car on sent bien que ces dimensions n'ont rien à voir avec celles de la bouteille et influençant son frottement dans l'air.

Mais ce doit être une dimension caractéristique de la bouteille alors pourquoi ne pas prendre le diamètre ? Puisque ça caractérise aussi la bouteille.
En fait, on choisit la dimension caractéristique au feeling ?

Estelle

Pas d'importance.

Dans tous les cas, tu vas trouver un nombre de Reynolds tel que le CX est dans sa portion constante (dans le cas de l'exercice).

C'est juste une estimation pour voir où on est.

Il suffit donc de prendre une mesure plausible pour la taille de la bouteille, c'est juste un bon ordre de grandeur dont on a besoin.

Evidemment, si le but était de trouver une valeur de CX extrêmemnent précise, ce serait différent, mais ce n'est pas le cas.
Et d'ailleurs, si on veut une valeur précise du CX, la seule manière de la trouver est de la mesurer en souflerie.
Pour une bonne approximation ce qui a été fait est suffisant.

Tu peux recommencer si tu veux avec 0,1 m au lieu de 0,3 m, mais tu vas aussi trouver qu'on est dans la partie constante de la courbe de Re.

D'accord

Et une fois qu'on a le nombre de Reynolds, la viscosité dynamique et la vitesse du fluide, comment on aboutit à Cx ?

Estelle

Une fois qu'on a le nombre de Reynolds ...

Il faut avoir les courbes, comme celles dont je t'ai donné le lien pour la sphère.
Et la courbe donne alors la valeur de CX à utiliser.

Et si on n'a pas les courbes pour la forme qu'on utilise, on fait une estimation "au pif" à partir des courbes de la sphère.

... Ou on mesure le CX en soufflerie, mais il faut encore avoir le matériel nécessaire et là ...
Aucune chance d'avoir un labo équipé qui te laissera faire (sans payer bien cher).

Il reste deux questions que je me pose.

* Comment calculer le maître couple ?

* >> pour déterminer l'expression de F :

Je n'ai pas lu le lien où on parle du F = ma, il me semble que c'est sans intérêt ici.

Comme je te l'ai déjà dit, le maître couple de la bouteille est la section de la bouteille vue par un observateur qui regarde la bouteille venir vers lui.

J'ai une bouteille de Coca plastique de 1,5 l prés de moi.

En gros, je mesure:
Diamètre de la partie cylindrique:  9 cm
hauteur de la partie cylindrique : 22 cm
partie en tronc de cône: grande base = 9 cm de diam , petite base (goulot) 3 cm de diam et hauteur = 8 cm

S = (9*22) + (1/2)*(9+3)*8 = 246 cm² = 246.10^-4 m²

S = 246.10^-4 m² (environ)

Pour F = ma, oui j'avais mal lu, je pensais que ça pouvait m'aider à expliquer d'où venait la formule F=...

Merci pour le maître couple, je vais essayer d'appliquer tout ça.

Estelle

Je ne sais pas quel est le but de l'exercice.

Mais, si on fait voyager une bouteille de plastique VIDE verticale, tu devrais trouver que la bouteille va, soit basculer, soit glisser sur le tapiss avec une vitesse de tapis assez petite.

Si la bouteille est pleine de liquide, alors, la bouteille restera stable pour des vitesses de tapis même assez grande.

Je l'avais résumé dans mon autre topic.

On fait voyager une bouteille de plastique verticale sur le tapis et on veut déterminer l'accélération limite pour qu'elle ne bascule pas au démarrage.

On a choisi un modèle et les calculs nous ont conduit à (H et R sont les coordonnées du centre de gravité de la bouteille).

Pourtant expérimentalement (et avec du bon sens) on se rend bien compte que si la bouteille est vide ou entièrement pleine (donc la position du centre de gravité ne varie pas), la stabilité de la bouteille n'est pas la même. En fait, on s'aperçoit que la masse influe sur la stabilité.

Ce qui signifie que le modèle ne convient pas... peut-être parce qu'on a négligé la résistance de l'air, la force de traînée. D'où ce topic.

Estelle

Un croisement ? C'est à dire que j'aurais interverti ?

Repère orthonormé (O,x,y) avec x orienté vers le haut et y vers la droite.
R est la coordonnée de G sur x et H celle sur Y.

Sauf erreur.

Estelle

Plus la bouteille et haute et a un petit rayon, plus facile elle est à basculer.

Donc le "a" max permis diminue avec la hauteur de la bouteille et augmente avec le rayon de la bouteille.

Pourquoi avoir pris ox vertical et oy horizontal, alors que l'habitude est inverse ?

R a l'air de valoir la demi hauteur de la bouteille et H son rayon dans ta formule.

Si c'est cela, c'est la meilleure façon d'être mal compris.

Je viens de m'apercevoir que je me suis trompée dans mes explications... (Ox) est l'axe horizontal et il est orienté vers la droite ; (Oy) est l'axe verticale et il est orienté vers le haut.

Désolée pour ces confusions.

Estelle

En relisant les calculs, j'ai trouvé l'erreur. Finalement, on a bien : l'accélération limite est proportionnelle au rayon et inversement proportionnelle à la hauteur.

Merci =)

Estelle

...

.

Estelle

C'est mieux, et dans cette formule, H est alors la distance entre le fond de la bouteille et le centre de gravité de la bouteille.

Fx = (1/2)*Rho*V²*S*Cx

Pour une bouteille en plastique de 1,5 L:

Fx = (1/2)*1,2*V²* 246.10^-4 * 1

Fx = 0,015. V²
-----
La masse d'une bouteille vide de 1,5 L de plastique est de environ 36 g

La force horizontale au niveau du centre de gravité de la bouteille due à l'accélération du tapis est donc F1 = 0,036 * a

La force horizontale due aux frottements aérodynamiques est Fx = 0,015.V²
---
Dans le cas de la bouteille pleine au aurait:

La force horizontale au niveau du centre de gravité de la bouteille due à l'accélération du tapis est donc F1 = 1,5 * a

La force horizontale due aux frottements aérodynamiques est Fx = 0,015.V²
-----

Il devrait être facile, connaissant l'accélération appliquée au tapis et le temps que dure cette accélération de calculer la vitesse max du tapis et de comparer les forces F1 et Fx.

Tu trouveras presque certainement que pour la bouteille pleine, Fx sera beucoup plus petit que F1 et donc l'effet de Fx sur le basculement de la bouteille est négligeable.

Mais dans le cas de la bouteille vide, Fx ne sera certainement pas négligeable devant F1 et donc les effets de Fx sont à prendre en considération dans le basculement de la bouteille vide.

Bonjour

J'ai lu tout ça et j'ai parfaitement compris =)

Merci beaucoup J-P, tu m'as beaucoup aidé et je suis t'en suis très reconnaissante !

Estelle

Bonjour

Après de nombreux mesures et calculs...
La vitesse du tapis est 0,15 m/s et l'accélération est de 1,5 m/s².
J'utilise une bouteille en plastique de 50 cL.

Je trouve :
Fx = 2.10^-4 N.
F1 (pleine) = 0,78 N.
F1 (vide) = 0,03 N.

Qu'en penses-tu ?

Estelle

Bouteille pleine : F1/Fx = 3900 => négligeable, c'est sûr.
Bouteille vide : F1/Fx = 150 => non négligeable... ?

Estelle

Je n'en pense pas grand chose de bon.

Si on a bien a = 1,5 m/s² et vmax tapis = 0,15 m/s

Si l'accélération était bien constante pendant la phase de démarrage, l'accélération se ferait sur un temps de 0,1 s

Et cela me parait bien court.
----
Pour que l'influence de Fx soit bien "sentie", il faudrait qu'on ai par exemple Fx > 0,2 F1 (au pif de nouveau)

Soit FX = 0,03 * 0,2 = 0,006 N

Or Fx = (1/2).Rho air * v² * S * Cx

Avec S = 110.10^-4 m² (environ pour une bouteille de 0,5 L)

Fx = 0,0066v²

0,0066v² = 0,006
v = 1 m/s environ.

Donc si vmax est vraiment de 0,15 m/s, l'effet de Fx sera trop petit (par rapport à celui de F1) que pour être vraiment remarqué.
-----

Verifie bien la vitesse MAX du tapis car 0,15 m/s est vraiment très faible.

En fait, je ne comprends pas vraiment la différence entre v et vmax ?

Ce qu'on veut éviter, c'est que la bouteille bascule au démarrage sous l'influence d'une accélération trop forte, et non pas qu'elle bascule pendant le transport à cause de la vitesse.

Estelle