c'est le - du "-g" qui m'embête...

Bonjour.

L'égalité est une égalité vectorielle.

L'égalité a = - g  est une égalité numérique qui résulte de la détermination des coordonnées du vecteur accélération sur des axes, avec, comme cela semble être le cas ici, un axe horizontal et un axe vertical , ce dernier orienté positivement vers le haut.

Dans ces conditions, on a :    et    car le vecteur est vertical vers le bas.

Au revoir.

Mais si par exemple prenons l'exemple d'un skieur, il descend vers le bas donc dans le sens du vecteur g pourquoi est ce toujours -g?

Mauvais exemple, si c'est un skieur qui glisse sur une pente, son accélération n'est pas égale à . Dans ce cas, il est plus commode de prendre un axe parallèle à la pente et un axe perpendiculaire à cette pente.

L'accélération n'est égale à que si le solide n'est soumis qu'à son poids (mouvement de projectile, chute libre etc...)

je ne comprends toujours pas d'ou vient le -... ca m'enerve

En fait vous ne maîtrisez pas la technique de détermination des coordonnées d'un vecteur.

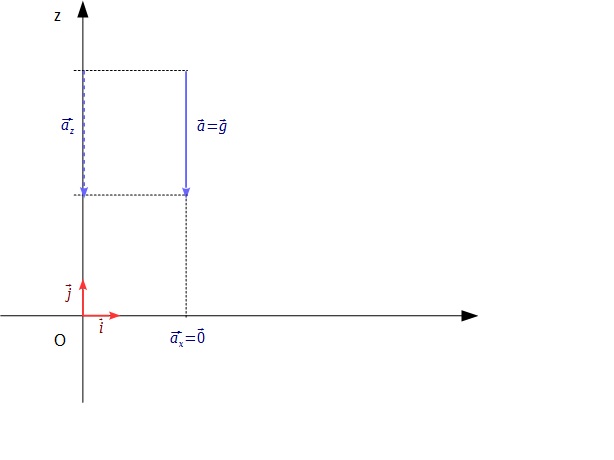
Sur le schéma ci-dessous, on a :

Les composantes du vecteur selon les axes et sont les vecteurs   et   tels que :  

Concernant , l'affaire est réglée puisque    on a donc :  

Pour , on peut écrire    puisque et sont colinéaires.

Comme et sont de sens contraires, sera négatif.

On aura donc :    ou encore :

Finalement, on pourra écrire :

et    sont les composantes de     les composantes sont des vecteurs.

et    sont les coordonnées de      les coordonnées sont des nombres.


Est-ce plus clair ?

Si j'ai bien compris alors cela veut que si l'axe Oz serait orienté vers le bas alors on aurait a = g

Oui, c'est bien cela.