Inscription / Connexion Nouveau Sujet
Absorption de la lumière par un marériau
Bonjour,
J'ai réellement besoin de votre aide, cela fait plusieurs jours maintenant que je suis sur un exercice,
et il m'est impossible de le finir. Je suis totalement bloquée et déçue de ne pas réussir à le faire.
Voici l'exercice :
L'absorption de la lumière lumière par un matériau est donnée par la loi de beer-Lambert. Cette loi établit une dépendance exponentielle entre l'intensité transmise ( lumière qui a traversé le matériau) et la longueur de l'échantillon tel que : I = I0.exp (-k.L)
Où I0 : l'intensité de la source avant de traverser l'échantillon (W.m^-2)
k : une constante caractéristique de l'échantillon
L : la longueur de l'échantillon ( en m)
On appelle A l'absorbance de cet échantillon tel que : A = k.L
1) Quelle doit être l'unité de k ? En déduire la dimension de A.
Rep : Pour l'unité de k, j'ai répondu que c'était en m.s^-1
Après pour A... Je suis perdue.
2)Des mesures de l'intensité transmise d'un rayonnement à travers un échantillon en fonction de sa longueur donnent les résultats suivants : ( cf document )
a) Modifier la formule de l'intensité afin que la fonction I = f(L) soit une droite.
Je ne comprend pas vraiment cette question...
b) Tracer sur papier millimétré la courbe I = f(L) après avoir choisi judicieusement les échelles. Déduire de la courbe ainsi tracée les valeurs de Ià=0 et de k.
En espérant pouvoir bénéficier de votre aide, et que vous puissiez m'aider à comprendre tout ça. Car avant lundi, je n'avais jamais vue cela donc je suis complètement perdue !
Merci de prendre le temps de m'aider à y voir plus clair,
Bonjour,
Pourquoi voudrais-tu que l'unité de k soit des mètres par seconde (homogène à une vitesse). Quel est ton raisonnement ?

Bonjour,
Je l'ai mis en mètre par seconde car comme A n'a pas d'unité et que L est en mètre ça m'a paru possible que se soit ça.
Il est en effet nécessaire que l'argument de exp(...) soit sans dimension.
Donc il faut que -k.L soit sans dimension
Puisque la dimension de L est une longueur, il faut que la dimension de k soit l'inverse d'une longueur.
Si tu exprimes L en mètres (m) il faut que k soit en m-1
Si tu exprimes L en millimètres (ce qui semble raisonnable étant données le tableau que tu postes) il faut que k soit en mm-1
Et ainsi le produit -k.L = A sera sans unité
__________
Il faut une équation du type a.L + b
Tu devrais trouver (indice : d'où vient la troisième ligne du tableau avec des valeurs - très approximatives - pour Ln(I) ? )

J'ai vraiment du mal à comprendre...
Je n'ai jamais fait cela avant et tout est nouveau alors je vais mettre du temps pour comprendre !
Donc je devrais mettre k en mètre -1 ?
POur la dernière ligne, c'est mon professeur qui nous a demandé de calculer LnI... J'ai pensée qu'en faisant, par exemple, ln(125) que j'ai arrondi à 5, je trouverai le résultat
Tu as arrondi de manière beaucoup trop "brutale"
Si
I = I0.exp(-k.L)
alors
Ln(I) = Ln(I0) -k.L
ou
Ln(I) = -k.L + Ln(I0)
Je pense que tu reconnais l'équation d'une droite...
Voici mon graphique :
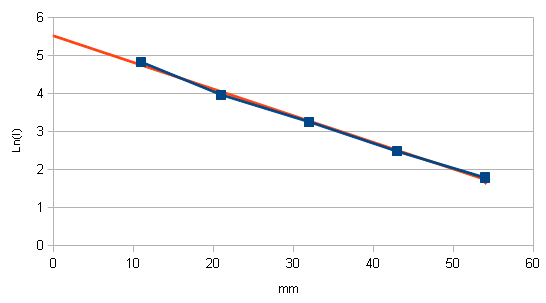
En bleu, les points { L (en millimètres) ; Ln(I) }
En rouge un segment de la droite d'équation
Ln(I) = -0,07 L + 5,518
L + 5,518
d'où l'on déduit
Ln(I0) = 5,518
I0 = exp(5,518)  249 W.m-2
249 W.m-2
k = 0,07 mm-1 ou k = 70 m-1

Merci pour l'aide, même si je ne comprend pas tout 
Comment avez vous trouvé que ln(I0) valait 5,518 ?
Merci pour le tableau, ça sera beaucoup plus précis pour le graphique 
J'aurais du laisser ce que m'indiquait la calculatrice !
L'équation de la droite que je te donne a été calculée par mon tableur. Régression linéaire par la méthode des moindres carrés à partir des données, c'est-à-dire à partir des points bleus qui ont pour coordonnées cles valeurs du tableau.
Les régressions linéaires par la méthode des moindres carrés sont au programme, changent de programme... Je ne sais pas en quelle classe on voit cela maintenant. Mais on peut s'en servir dans son tableur sans en connaître la théorie !

Merci pour les explications.
Oui c'est possible que se soit dans le programme. Je n'en connais rien car mon soucis est que je viens d'un bac STSS et qu'en ce moment je suis dans une licence aménagée SVTE pour nous remettre à niveau par rapport au baccalauréat scientifique, sauf qu'en cours de physique, il ne nous donne pas les bases, et nous donne directement ce genre d'exercice sens qu'on ne l'ai jamais vu.
Voila pourquoi je suis complètement perdue ! 
J'espère que tu connais le logiciel (gratuit) Sine qua non qui est une grande vedette (à juste titre) du site de l'île des maths.
Voici ce qu'il me donne :
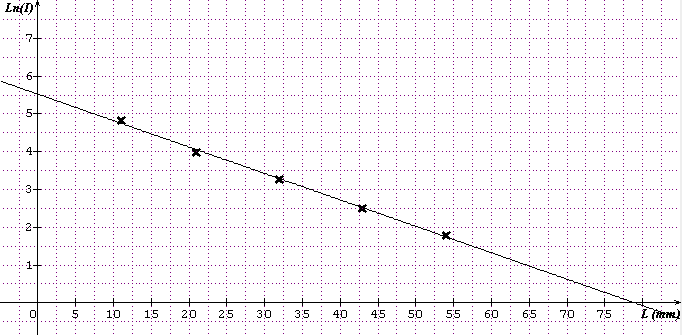
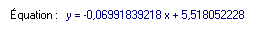

Non, je ne connaissais pas, mais je vais m'y intéresser.
L'equation en bas du tableau est la dimension de A ?
L'équation en bas du tableau est ce que donne le logiciel Sine qua non : 
![]()
J'ai rentré les coordonnées des points (voir le tableau) et j'ai demandé la régression linéaire. Il fait le graphique et donne l'équation de la droite.
Tu reconnais le coefficient directeur de la droite -0,0699 que j'ai arrondi à -0,070 mm-1
et tu reconnais l'ordonnée à l'origine : 5,518
C'est Ln(I0)
et donc
I0  exp(5,518)
exp(5,518)  249 W.m-2
249 W.m-2

La dimension de L est une longueur (unité SI le mètre ; le millimètre semble un bon choix ici)
La dimension de k est celle de l'inverse d'une longueur. Donc mm-1 si L est en millimètres
A n'a pas de dimension puisqu'il est le produit d'une longueur par l'inverse d'une longueur
I et I0 sont des intensités lumineuses dont l'unité est le watt par mètre carré (W.m-2)
Il est indispensable pour tes études de comprendre les grandeurs, les dimensions, les unités... tout ceci est à la base de la physique.



