Salut!

Tu es sûr(e) de la relation? N'y aurait-il pas un problème de signe?

Oui , normalement la vitesse est toujours positive

certes oui mais cette relation est relativement rare, on ne l'utilise pour ainsi dire...jamais. On préfère utiliser les dérivées de quantités de matières respectant justement les signes... Ou els dérivées de vitesses.

Si tu établit ce tableau :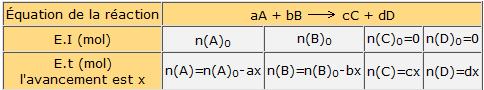

Tu obtiens directement cette relation :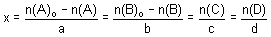

d'où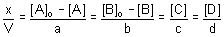

et avec v = 1/V*dx/dt...

J'ai pas bien compris !! et si on voulait trouver la vitesse de "a" en sachant la vitesse de c , on ferait comment ?!

Je t'ai dit ce qu'il fallait utiliser,je n'ai rien démontrer. Maintenant c'est à toi d'utiliser ces relations pour démontrer ce que tu cherches, il n'y a rien à comprendre

Va=1/.d[a]/dt , Vc= 1/. d[c]/dt ... et après ? je ne sais pas comment on trouve va/ = vc/ , et encore comment on trouve la vitesse de c en ayant la vitesse de a ?! je ne sais pas non plus

merci pour votre aide  

Là tu vas tourner en rond, part plutôt de la relation avec l'avancement

je part comment et pour arriver ou ?!

Tu pars de x/V = ... pour en arriver à ce que tu cherches

je cherche la vitesse de c et je ne vois absolument pas comment je puisse la trouver en commençant avec x/V =...