Inscription / Connexion Nouveau Sujet
Vitesse minimale
Salut tout le monde
Je n'arrive pas à résoudre cet exercice. Pouvez vous m'aider s'il vous plait ?
Exercice
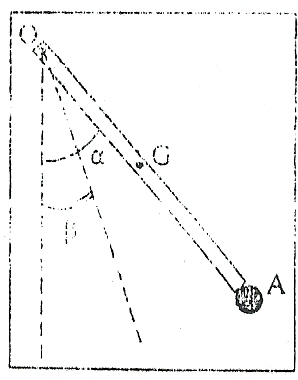
Une barre homogène OA de masse m = 400 g de centre d'inertie G et de longueur l = OA = 1 m est mobile autour d'un axe ( ) horizontal passant par son extrémité O.
) horizontal passant par son extrémité O.
Son moment d'inertie par rapport à ( ) est J
) est J = (1/3) × m l²
= (1/3) × m l²
La barre est munie d'une charge quasi ponctuelle de masse m' = 200 g
1. Le système constitué est écarté de sa position d'équilibre stable d'un angle  = 60° puis abandonné sans vitesse initiale .
= 60° puis abandonné sans vitesse initiale .
1.1 Déterminer la vitesse V1 du système au passage de la position d'angle  = 20° par rapport à la verticale.
= 20° par rapport à la verticale.
1.2 En déduire la vitesse V2 du système au passage de sa position d'équilibre stable
2. Le système étant au repos dans sa position d'équilibre stable , calculer la vitesse minimale à lui communiquer pour qu'il fasse un tour complet
On donne : g = 10 N/kg
Pouvez vous me donner les directives pour réussir à résoudre l'exercice ? Merci d'avance
Salut,
Une méthode pour y arriver est d'utiliser le principe de conservation de l'énergie mécanique pour ensuite en déduire une vitesse :
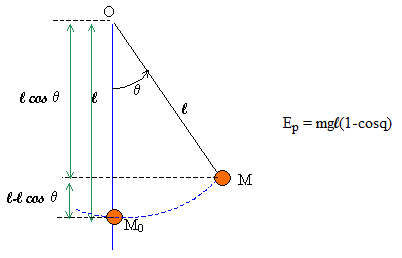
(image extraite du site chimix.com)
A toi  !
!
J'aimerais utiliser ici seulement le théorème l'énergie cinétique.
Ici Ec en M est il ? Ec = 1/2(m+m')V1² ? ou Ec = 1/2 J
 ² ?
² ?
Dans ce cas, il faut exprimer le moment d'inertie du solide {tige + barre} par rapport à l'axe ( ).
).
A partir de là tu pourras exprimer le théorème tel que tu le connais.

Vous parlez de quelle tige ? Je pense que le moment d'inertie du système { barre + charge quasi ponctuelle } est 1/3 m l²
Non, l'énoncé te dit que ça concerne la barre, pas la masse ponctuelle. Il faut donc bien à mon sens ramener son moment d'inertie à  non ?
non ?
As-tu entendu parlé du théorème de Huygens ?
Ok le moment d'inertie du système { barre+tige} est il (1/3) × m l² ?
Non je n'en ai pas entendu parler.
1/2 × (1/3 m l² ) ×  ² = m g×(l/2)cos
² = m g×(l/2)cos + m g×lcos
+ m g×lcos ?
?
Je voudrais vous demander : en fait lorsqu'on est dans un mouvement en rotation ; le travail du poids est il toujours m×g×h ou il devient M(moment)× ? C'est la même aussi pour le travail du ressort ?
? C'est la même aussi pour le travail du ressort ?
Pour ma part, je dirait que sauf erreur
Pour répondre à ta question, tout dépend de l'utilisation que tu fais du théorème.
Si tu relis la partie I de cette fiche : ![]() , tu peux l'écrire de deux façons :
, tu peux l'écrire de deux façons :
* soit sous la forme d'une dérivée de l'énergie cinétique du système : on l'appelle aussi théorème de la puissance, et dans ce cas dEc/dt = somme des puissances appliquées au système.
* soit sous la forme différentielle, et dans ce cas la différence d'énergie cinétique entre un état initial et final est égale à la somme des travaux des forces appliquées au système.
Il y a aussi une troisième méthode pour les solides en rotation autour d'un axe fixe qui est le théorème du moment cinétique pour un solide en rotation autour d'un axe fixe :
J/dw/dt = somme des moments des forces par rapport à l'axe  appliqués au système.
appliqués au système.
W(P) = m.g.h ne veut rien dire, il faut que tu reviennes à la définition du travail d'une force.
Ok mais d'où vient m' × l² ?
Mais dans ce cas ici quelle est l'expression du travail du poids ?
Est ce que ce serait possible d'aller plus rapidement ? Merci de votre aide
Re,
Comme je ne vois pas vraiment ce que tu abordes en cours, je vais procéder ainsi :
* Système : pendule de masse (m + m') ;
* Référentiel : terrestre supposé galiléen ;
* Bilan des forces : le poids du pendule exercé en son centre d'inertie.
Etape 1 Le première étape consiste à déterminer l'expression de la distance du point d'articulation
au centre d'inertie
:
.
Etape 2 :
* je suppose que l'articulation au niveau de 0 est une liaison parfaite donc le travail des actions de liaison exercées par sur le pendule est nul. De même pour le moment.
* Le pendule est un solide en rotation autour d'un axe fixe , donc le théorème de l'énergie cinétique s'écrit entre l'instant initial (
, vitesse nulle) et l'instant où le pendule atteint
:
* La seule force conservative ici est le poids exercé sur ce pendule donc --> cf. le premier schéma que je t'avais proposé (message du 21/11 à 20h19).
* Or à l'état initiale la vitesse est nulle donc .
Finalement,
Sauf distraction de ma part 
Pour la question 2 :
Je considère un angle quelconque
L'énergie mécanique peut s'écrire :
est supérieure ou égale à
donc l'énergie mécanique est supérieure ou égale à l'énergie potentielle de pesanteur
.
Ainsi, si l'angle
n'est pas borné et le pendule peut faire des tours entiers autour de
.
Si on revient au mouvement d'oscillation défini plus haut.

Ok je comprends gbm . En fait je n'avais pas compris l'énergie mécanique puisque je n'ai pas encore fait la leçon. Maintenant je comprends mieux car j'ai essayé de faire l'exercice aujourd'hui .
Re,
Finalement,
Sauf distraction de ma part

Donc ici pour le calcul du travail du poids on doit additionner les masses ? Moi j'avais calculé séparément le travail du poids de la barre et le travail du poids de la charge quasi-ponctuelle .Mais ici sachant que nous sommes dans un mouvement de rotation pourquoi le travail de chaque force ne se calcule de cette manière W = M×
 ? ( M est le moment de la force )
? ( M est le moment de la force )
Merci gbm pour votre aide !
Bonsoir Sid07,
En fait je n'avais pas compris l'énergie mécanique puisque je n'ai pas encore fait la leçon
Energie mécanique = énergie cinétique + énergie potentielle.
Donc ici pour le calcul du travail du poids on doit additionner les masses ?
En fait j'ai calculé la distance d = OG du centre de masse (centre d'inertie) de l'ensemble {barre + masse ponctuelle}, d'où pourquoi j'ai sommé les masses en ce point.
Mais ici sachant que nous sommes dans un mouvement de rotation pourquoi le travail de chaque force ne se calcule de cette manière W = M×
 ( M est le moment de la force )
( M est le moment de la force ) Pour rappel, par définition du produit scalaire, le travail du poids se simplifie de la façon suivante :
Le travail du poids d'un corps est donc indépendant du chemin suivi lors de son déplacement, il ne dépend que de la variation d'altitude du centre de gravité de ce corps.
cf. mon schéma du 21-11-15 à 20:19

J'ai du mal à saisir pour le travail du poids, dans toutes les situations ( translation ou rotation ) W(P) =  mg(zB - zA) ?
mg(zB - zA) ?
OUI !
Et comme le travail du poids d'un corps est donc indépendant du chemin suivi lors de son déplacement, il ne dépend que de la variation d'altitude du centre de gravité de ce corps, si je le fait pour un angle donné, je fais intervenir la trigonométrie (au signe près) :

(image extraite du site chimix.com)

Dans mon exercice j'ai mis :
Comme il y a deux forces motrices qui s'exercent sur le système ( barre+charge ponctuelle ) en appliquant le théorème de l'énergie cinétique
1/2×J ×
×  ² = m'×g × l× (cos
² = m'×g × l× (cos - cos
- cos ) + m×g × l/2 × ( cos
) + m×g × l/2 × ( cos - cos
- cos )
)
Est ce que j'ai fais est il juste ?
OUI TB !
Tu fais bien dans chaque cas la différence d'altitude entre l'état initial et l'état final (en utilisant des projections via la trigonométrie).

bonjour a tout le monde je voulais demander si on ne pouvait pas passer par la cinétique pour résoudre cet exercice



