Inscription / Connexion Nouveau Sujet
Un archer ...
Un archer veut toucher une cible située approximativement à 30 mètres horizontalement et 20 mètres verticalement. Sachant que l'archer tire avec un angle de 38° par rapport à l'horizontale, quelle vitesse en km/h devra t'il donner initialement à sa flèche pour qu'elle atteigne sa cible? En combien de temps la flèche atteindra sa cible?
Merci.
L'énoncé ne précise pas si la cible est plus haut ou plus bas que l'archer.
Les 2 cas sont cependant possibles.
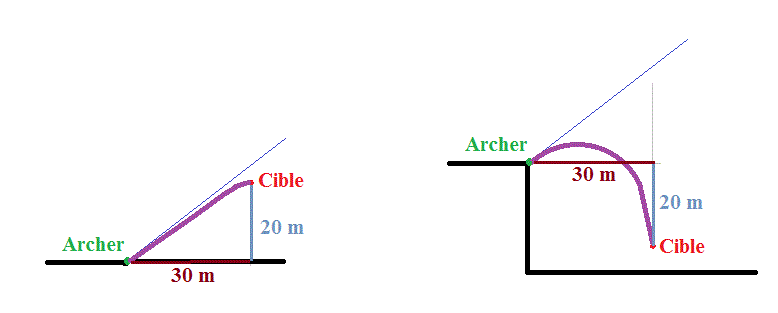
Lequel faut-il considérer ?
Dans le repère adéquat (... que tu décriras).
La position de la flèche est donnée par ses coordonnées en fonction du temps.
x = Vo.cos(38°).t
y = Vo.sin(38°).t - gt²/2
Et il faut que pour une certaine valeur t1 de t, on ait x(t1) = 30 et (t1) = 20
Soit donc :
Vo.cos(38°).t1 = 30
Vo.sin(38°).t1 - g.t1²/2 = 20 (avec g = 9,8 N/kg)
On élimine t1 entre ces 2 équations.
t1 = 30/(Vo.cos(38°))
Vo.sin(38°)* 30/(Vo.cos(38°)) - 9,8*(30/(Vo.cos(38°)))²/2 = 20
30.tan(38°) - 9,8*(30/(Vo.cos(38°)))²/2 = 20
9,8*(30/(Vo.cos(38°)))²/2 = 30.tan(38°)) - 20
(30/(Vo.cos(38°)))² = 0,702
30/(Vo.cos(38°)) = 0,8377
Vo = 30/(0,8377 * cos(38°))
Vo = 45,4 m/s
et t1 = 30/(Vo.cos(38°)) = 30/(45,4*cos(38°)) = 0,84 s
A toi de comprendre et remettre tout cela en forme.
Sauf distraction.
Annuler
connectez vous