Inscription / Connexion Nouveau Sujet
Trombone de Koenig
Bonjour est-ce-que qqn pourrait m'aider à faire cette exercice svp parceque je ne comprends pas.
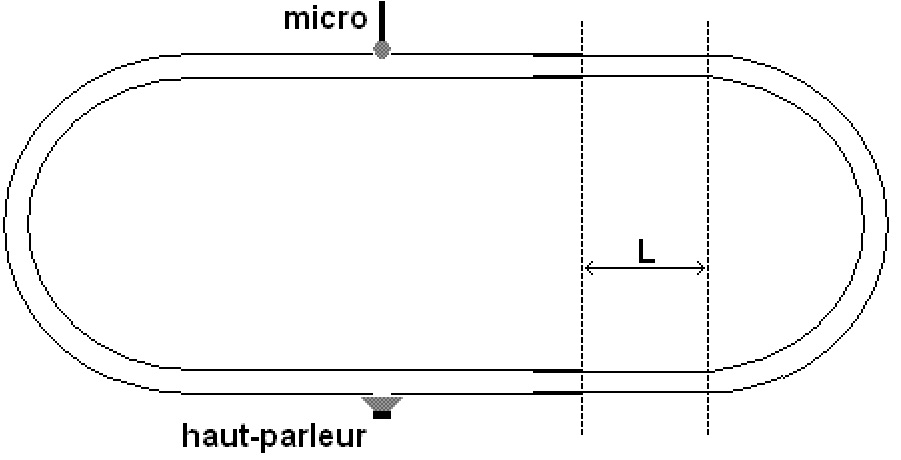
Énoncé : le trombone de koenig est un dispositif expérimental permettant d'obtenir des interférences sonores. En effet, les ondes émises par le haut-parleur suivent deux trajets différents dans chaque branche du trombone et peuvent arriver au micro avec un dephasage. Grâce à la coulisse, on peut régler la longueur d'un des deux trajets.
Le haut parleur diffuse une onde sinusoidale de fréquence 880Hz on observe un maximum d'amplitude sur le microphone si L=0.77m et L= 1.35m
questions:
-Combien de positions du tube conduisant à un maximum d'amplitude peut on trouver entre ces deux valeurs?
-Donner une position pour laquelle l'onde captée possède une amplitude minimale avec une onde de fréquence f=760Hz
Bonsoir,
Bien que cela ne soit pas précisé, je suppose que le trombone est rempli d'air et qu'on te donne ( ou que tu es censée connaître) la célérité du son dans l'air à la température à laquelle se font les mesures.
Les maximums d'amplitude sont observés lorsque la différence des longueurs des trajets parcourus par l'onde sonore est un multiple entier de la longueur d'onde.
En termes mathématiques : d2-d1 = k.
Les minimums d'amplitude sont observés pour d2-d1=(2k+1)./2
Par construction de l'appareil lorsque la longueur mesurée est égale à L la différence d2-d1 = 2L
k : nombre entier
: longueur d'onde du son calculable à partir de sa fréquence et de sa célérité.
Bonjour désolé de te déranger mais je n'ai pas compris ce que odbugt1 a expliqué, j'ai cet exercice à faire et je n'y arrive pas Pourrais tu m'éclairer ? 
Bonsoir oui bien sûr, alors pour la Q1 il faut trouver les deux valeurs entre k4= 2lambda et k7 donnée par l'énoncé.
J'espère t'avoir aidé.
Oui merci bcp j'y ai finalement réussi, je trouve 0,975 et 1,17 m mais je ne sais pas commencer la Q2.
Merci beaucoup de répondre ^^
Bonsoir,
@Lamii
Je précise et complète la réponse de Ainaa.
N'ayant pas de précision dans l'énoncé j'utilise c=340m/s pour la célérité du son dans l'air.
La longueur d'onde d'un son de fréquence 880Hz est : =c/f = 340/880 = 0,386m
Les maximums d'amplitude sont tels que d2-d1 = k ( k est un nombre entier)
Le trombone de Koenig est construit de façon que d2-d1=2L
donc k = 2L et k = 2L/
L'énoncé indique un maximum d'amplitude pour L = 0,77m ce qui donne k=2*0,77/0,386 
4
Un autre maximum est observé pour L = 1,35m ce qui correspond à k=7
On peut donc observer 2 autres positions comprises entre 4 et 7 qui correspondent à k=5 et k = 6
On peut même calculer (mais ce n'est pas demandé) les valeurs de L qui correspondent à ces valeurs intermédiaires.
Pour k = 5 on aura L=5/2=5*0,386/2 = 0,96m
Pour k = 6 on aura L'=3=3*0,386 = 1,16m
Bonsoir odbugt1,
Merci beaucoup de mieux avoir détaillé je trouve les mêmes résultats mais la rédaction est largement meilleure.
Cependant j'ai une question pour la Q2, est ce que il faut changer lambda car on change de fréquence ?
Question 2
- Calculer la nouvelle longueur d'onde
- Appliquer la condition de minimum d'amplitude : d2 -d1 = (2k+1) /2
- La construction de l'appareil impose toujours d2 -d1 = 2L
- choisir une valeur entière pour k
- Calculer la valeur de L correspondante.
Annuler
connectez vous