Inscription / Connexion Nouveau Sujet
Travail exercée par un enfant sur une balançoire.
Bonjour ,
Merci d'avance. 
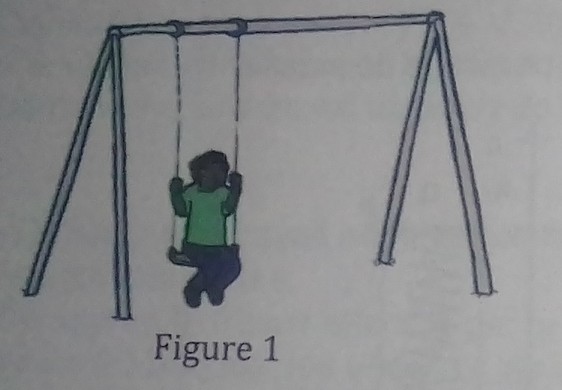
Le schéma ci dessous indique un enfant entrain de faire de la balançoire.(Figure 1).
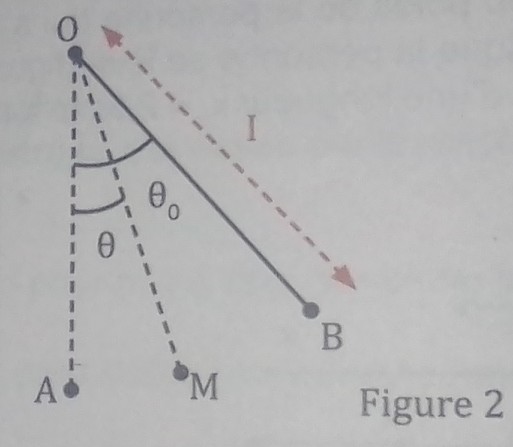
Sur la figure 2 , l'enfant de masse m=15kg est représenté par un matériel , quand les deux cordes de la balançoire vues de profil , de longueur chacune , de masse négligeable, sont assimilées à une seule corde au bout de laquelle l'enfant se situe.
θ0 , l'angle entre la position verticale et la position maximale où s'élève le centre d'inertie du système (l'enfant) avant de redescendre.
θ , l'angle entre la position verticale et la position où se trouve le système au point M à une date quelconque.
g=9,81 N/kg , l'intensité de la pesanteur.
1) Faire l'inventaire des forces appliquées à l'enfant sur la balançoire.
2) Montre que l'action mécanique exercée par les cordes sur l'enfant a un travail nul.
3) Déterminer l'expression du travail du poids de l'enfant , du point B au point P, en fonction de g , l , θ et θ0.
4) Déduire de la question précédente , la valeur du travail du poids de l'enfant du point B au point A.
Réponse.
1) Inventaire des forces :
-Le poids de l'enfant.
-La réaction du support sur lequel l'enfant est assis.
- La tension des cordes de la balançoire .
2) L'enfant assis sur la balançoire exercice un travail sur la balançoire. Pas le contraire donc l'action mécanique exercée sur par les cordes sur l'enfant a un travail nul.
3)
C'est là que je bloque ..
Inventaire des forces :
L'énoncé précise " Une seule corde au bout de laquelle l'enfant se situe "
Donc aucun support sur lequel l'enfant est assis.
Question 2 :
Contrairement à ce que tu écris la corde (qui représente en réalité 2 cordes) est en contact avec l'enfant et exerce donc bien une action mécanique sur lui
Question 3 :
La relation que tu évoques s'applique un déplacement rectiligne du point d'application du poids. Ce n'est pas le cas ici. Elle ne peut pas être utilisée.
Revoir : ![]()
Ok ,
2) Comment devrais je faire ?
3) Je n'arrive pas à lire l'intégralité à part quelques mot et images qui s'affichent ..
Question 2 :
Le point M se déplace depuis B vers A
Quelle est la nature de sa trajectoire ?
A un instant précis quelconque que dire de la direction du déplacement de M ?
A cet instant là que dire de la direction de la tension de la corde ?
Conclusion ?
Pour aider à répondre je conseille de faire un schéma faisant apparaître:
a) La trajectoire de M entre B et A
b) Le point M lui même à un instant précis (n'importe où entre B et A ) et la corde OM
b) la direction prise par M à cet instant précis.
c) Le vecteur tension de la corde au même instant.
Le point M se déplace depuis B vers A
Quelle est la nature de sa trajectoire ?
Je dirais (un peu) circulaire ..
A cet instant là que dire de la direction de la tension de la corde ?
Conclusion ?
Je ne sais pas ..
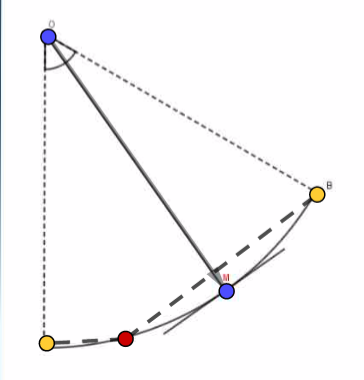
Pour t'aider je te joins un schéma volontairement incomplet.
Tu y trouveras en pointillés la position de la corde (OB) au moment ou le mouvement commence et sa position (OA) quand elle passe par la verticale.
Tu y trouveras aussi la position de la corde (OM) à un instant quelconque.
La trajectoire de M est l'arc de cercle BA
La direction suivie par M change tout le temps, mais elle reste toujours portée par la tangente en M à la trajectoire.
Il te faut ajouter le vecteur qui représente la tension de la corde au point M et essayer de répondre aux questions que je t'ai posée dans mon précédent post.
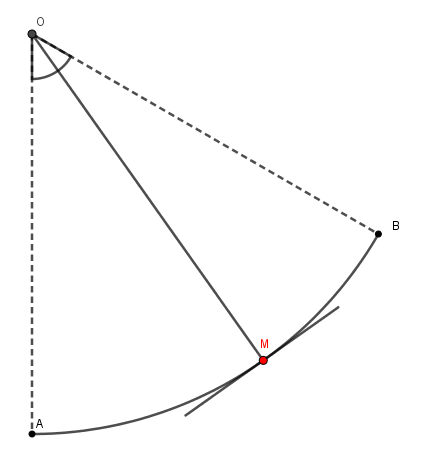
Non.
Relis la question 2 : Il s'agit de la tension exercée par la corde sur l'enfant.
A mon sens, les pointillés que tu as ajouté n'ont aucun intérêt.
Les points O, B, M et A qui sont ceux de l'énoncé sont évidemment bien placés !
Le point rouge que tu as ajouté n'a aucun intérêt pour répondre à la question posée.
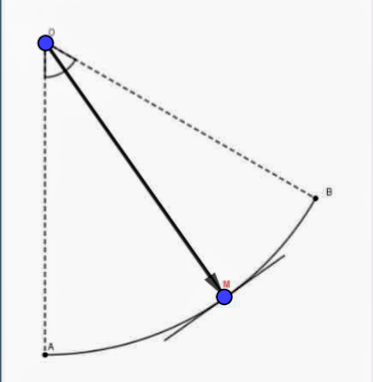
Il te faut maintenant placer correctement le vecteur tension de la corde exercée en M par cette corde sur l'enfant
Tu n'as pas tenu compte de mon message du 16-08-20 à 17:59
Il te faut représenter le tension de la corde exercée sur l'enfant et pas sur le point O comme tu l'as fait.
Remarque : Ce n'est pas une bonne idée de donner au vecteur tension de la corde une longueur qui occupe toute la longueur de la corde. Cela risque d'engendrer des confusions.
Au sujet du vecteur représentant la force exercée par la corde sur l'enfant (tension de la corde) :
a) Quel est son point d'application ?
b) Quelle est sa direction ?
c) Quel est son sens ?
Les réponses à ces trois questions devraient te permettre de représenter correctement ce vecteur et de déduire de la figure obtenue la raison pour laquelle le travail de cette force est nul.
Au sujet du vecteur représentant la force exercée par la corde sur l'enfant (tension de la corde) :
a) Quel est son point d'application ?
Le point M
b) Quelle est sa direction ?
Verticale
c) Quel est son sens ?
Du haut vers le bas (Du point O vers le point M )
Au sujet du vecteur représentant la force exercée par la corde sur l'enfant (tension de la corde) :
a) Quel est son point d'application ?
Le point M
Oui
b) Quelle est sa direction ?
Verticale
Non. La tension de la corde a la même direction que la corde elle même.
Comme la direction de la corde change au cours du mouvement, le vecteur tension a aussi une direction qui change au cours du mouvement.
c) Quel est son sens ?
Du haut vers le bas (Du point O vers le point M )
Non. Je n'en finis pas de te répéter qu'il s'agit de la force exercée PAR la corde SUR l'enfant
Peux tu maintenant représenter la force exercée par la corde sur l'enfant ?
Non.
Relis les réponses aux points a) b) et c et dessine un vecteur en accord avec ces réponses .
(17-08-20 à 10:07)
et tiens compte de ma remarque 16-08-20 à 21:02 !
Si tu parles de mon schéma j'ai défini le 16-08-20 à 00:16 ce que sont " les traits en pointillés"
Je te rappelle que l'énoncé dit clairement que les deux cordes de la balançoire, vues de profil, sont assimilées à une corde unique.
Tout se passe comme si l'enfant se balançait accroché à l'extrémité inférieure d'une corde unique.
En d'autre termes le système {corde / enfant} se comporte comme un pendule simple sans frottements, ni résistance de l'air.
L'enfant décrit l'arc de cercle BA, avant de remonter de l'autre côté mais la remontée n'est pas étudiée ici.
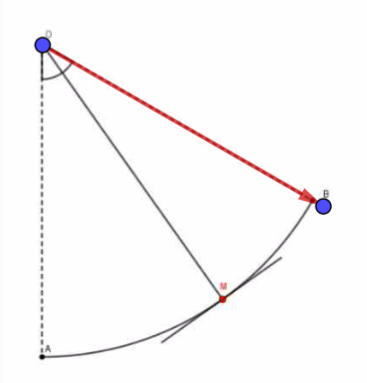
La corde exerce un force sur l'enfant.
Cette force s'exerce donc en M, elle a la même direction que celle de la corde, son sens va de M vers O (et non l'inverse)
On ne connait pas la valeur de cette force, elle sera donc représentée par un vecteur de longueur quelconque.
Le but de cette question est de montrer que cette force ne travaille pas.
Pour cela il te faut ajouter à ma figure (16-08-20 à 00:16) le vecteur . Rien de plus, rien de moins.
C'est à partir de cette figure qu'on constatera que le travail de est nul.
Non.
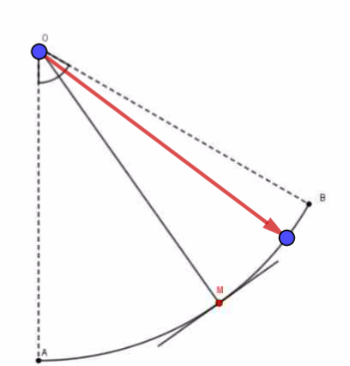
Comme déjà indiqué à plusieurs reprises le vecteur :
- a pour point d'application le point M
- est dirigé de M vers O et non l'inverse.
- N'a pas à avoir une longueur correspondant à la longueur de la corde.
Vas tu finir par en tenir compte ?
L'enfant, au bout de la corde en M est soumis à deux forces :
Son poids non représenté ici qui exerce son action vers le bas et l'action
de la corde qui "tire" l'enfant vers le point O
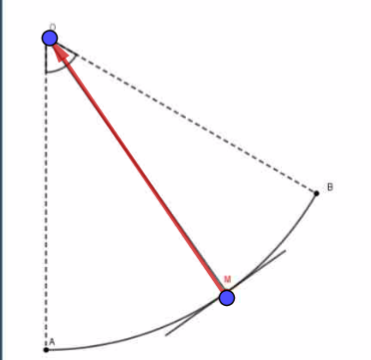
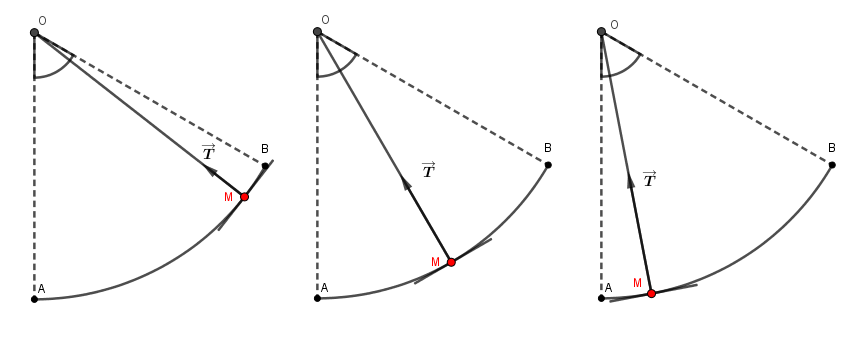
Sur le schéma ci-dessous la corde est représentée 3 fois
De gauche à droite :
a) Une fois, peu après son départ
b) Une deuxième fois à peu près à mi course
c) Une dernière fois un peu avant son passage à la verticale.
La direction suivie par le point M est dans tous les cas portée par la tangente à la trajectoire.
Qu'est ce qui permet d'affirmer que le travail de entre B est A est nul ?
Ah d'accord
Le travail de T est nul car est de même sens et direction que le vecteur accélération.
Ainsi le travail de la force est nul car le produit scalaire de deux vecteurs perpendiculaires est toujours nul.
Tu tournes autour de la bonne explication sans y parvenir pour l'instant.
Il n'existe que trois cas dans les quels le travail d'une force est nul :
a) Si la force a une intensité nulle ( évident mais sans grand intérêt )
b) Si le point d'application de la force ne se déplace pas. Ce n'est pas ce qui se produit ici puisque le point M se déplace sur l'arc de cercle BA
Quel est le troisième cas ?
La tension T est perpendiculaire à la trajectoire donc son travail est nul car un produit scalaire est nul lorsque deux vecteurs sont perpendiculaires.
Super ! 
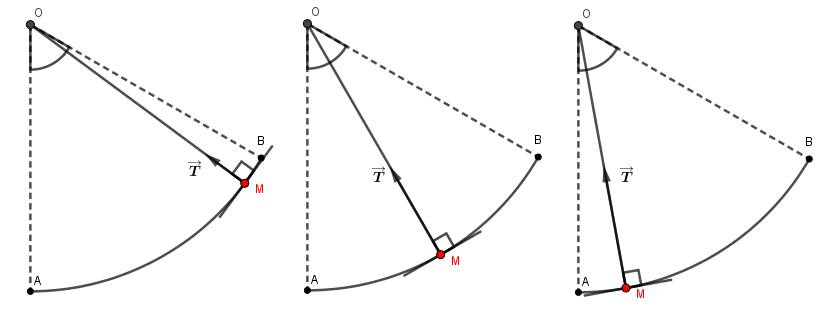
En effet, si la direction de la tension change sans cesse au cours du mouvement, il en va de même pour la direction du déplacement de M, mais ces deux directions restent constamment perpendiculaires (voir schéma)
Il en résulte que le travail de la tension est nul. Cette force ne participe pas et n'entrave pas non plus le mouvement de M.
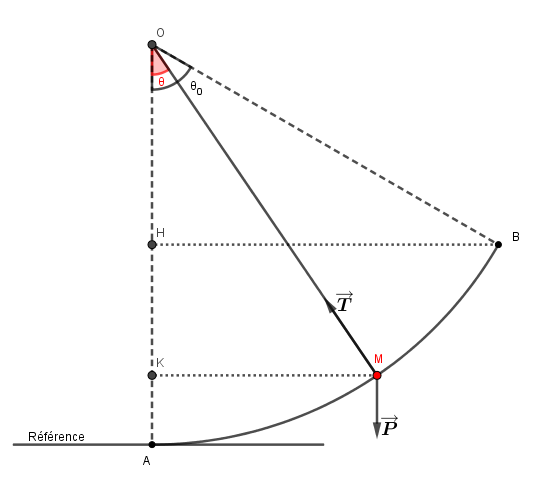
3) Déterminer l'expression du travail du poids de l'enfant , du point B au point M, en fonction de g , l , θ et θ0.
On utilise la relation dans laquelle zB et zM sont les altitudes des points B et M par rapport à un plan horizontal de référence que tu auras préalablement choisi et défini.
Tu confonds "référentiel" et "repère"
Je te conseille vivement de réviser ces notions fondamentales.
Il s'agit ici de choisir un plan horizontal à partir du quel seront comptées les altitudes.
Je suggère de choisir le plan horizontal passant par A, mais le choix reste libre.
Avec ce choix tu as (par exemple) zA = 0, zO = L (longueur du câble)
Tu as besoin de trouver zB et zM en fonction de L, θ et θ0 pour répondre à la question posée.
Le calcul de zB-zM en fonction de L, θ et θ0 relève de la géométrie et de la trigonométrie.
Calcule avec le secours de la trigonométrie zB, zM puis zB - zM
Rappel :
En prenant le plan horizontal passant par A comme référence des altitudes :
zA = 0 ; zO = L
Comme, hélas, bien trop souvent tu ne justifies pas tes résultats.
Il en résulte que je peux pas localiser la nature de tes erreurs et t'expliquer leurs origines.
Tu travailles donc contre tes intérêts.
Un simple coup d'œil et tu aurais pu constater par toi même que tes résultats sont faux.
En effet tu y additionnes (au numérateur de tes fractions) des longueurs avec des angles.
Pourtant tu sais probablement qu'on ne peut additionner que des grandeurs de même nature.
Indication supplémentaire sous forme de question :
Quelle relation existe t'il entre zB et zH (d'une part) et entre zM et zK d'autre part ?
C'est exact.
Il suffit donc d'exprimer zH en fonction de L et θ0 pour avoir zB
C'est à la portée d'un élève de 3ème (Système français)
Désolé
Alors j'ai considéré le triangle OHB rectangle en H.
ZH est égal au côté adjacent ×la longueur OB.
J'aurais dû dire que ZH=L×cos θ.
Tu es sur la bonne voie :
Dans le triangle OHB on a HO = L * cos(θ0) et non HO = L * cos(θ)
Mais ce n'est pas terminé car zH n'est pas égal à HO !
Je ne suis pas du tout à l'aise là ..
Je ne comprends rien , tu pourrais faire un exemple s'il te plaît ?