Bonjour,
Merci d'exposer, conformément au règlement de ce forum, d'exposer ce que tu as fait avant de demander de l'aide.

Désolé,  je l'avais homis. Voici ce que j'ai fait:
J'ai calculé l'angle de la pente en multipliant le pourcentage par 3,6 ça m'a 4.8
Puis j'ai appliqué le principe d'inertie comme demandé à la voiture seulement faisant la projection des forces.
-Psin + f'= F
Ce qu'à donné une valeur négative. Cela étant impossible puisque F n'est pas résistante mais motrice.  C'est la ou j'ai des difficultés

Voici mon schéma pour le principe d'inertie appliqué à la voiture

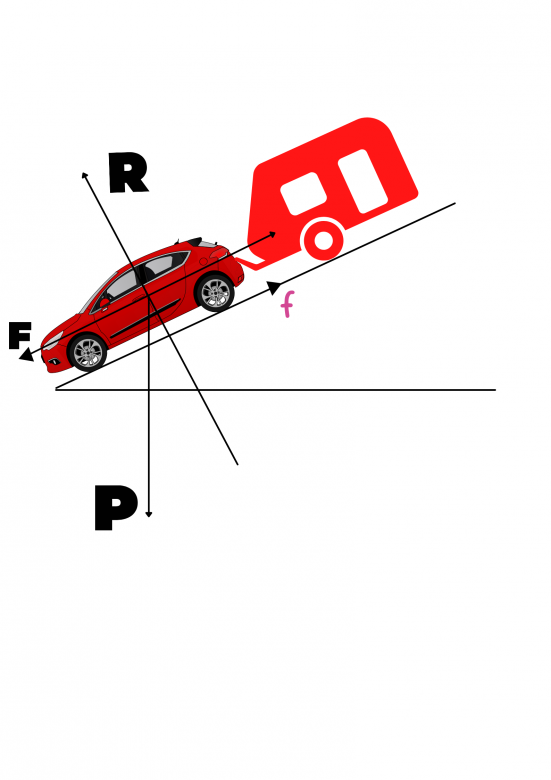
5 forces s'exercent sur la voiture.
La première chose à faire est d'identifier ces 5 forces.
Ecrire ensuite le principe d'inertie et projeter la relation vectorielle obtenue sur un repère bien choisi.

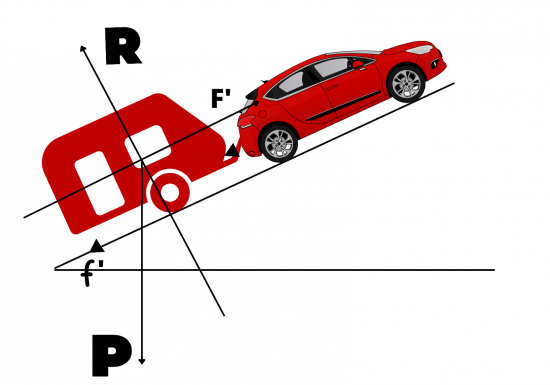
Remarque : L'énoncé indique que la voiture tracte la caravane en montée. Ton schéma fait apparaitre une descente.

Merci je le fais puis je vous reviens

Bon je fais ce que vous avez dit mais j'arrive pas a trouver l'intensité de la cinquième force je voulais envoyé le schéma  ici mais je me suis trompé et le règlement interdit le multi-post mais vous avez vu le schéma  je pense

J'ai fais ce que vous avez dit mais je me suis trompé en l'envoyant la cinquième force c'est la tension je pense.  Mais comme je n'ai pas déterminer son intensité. Je l'ai fais sans la tension:
Fsin+f

5 forces (dont une motrice, une neutre,  et trois résistantes) s'exercent sur la voiture.
- La force motrice   
- Le poids de la voiture
- La réaction normale exercée parla route.
- La force de frottement  
- La force exercée par la caravane sur la voiture.

Le mouvement de la voiture étant rectiligne et uniforme on applique le principe d'inertie :
  +   +  +  +  =   

Dans le schéma ci-dessous la voiture est représentée par son centre de gravité G. La caravane qui ne fait pas partie du système étudié n'est pas représentée.

Il te faut maintenant projeter la relation vectorielle ci dessus.

Ce qui me donnera:
F: Psin+F'+f

Mais l'intensité de F' pour la déterminer il faudrait qu'on utilise l'autre système?

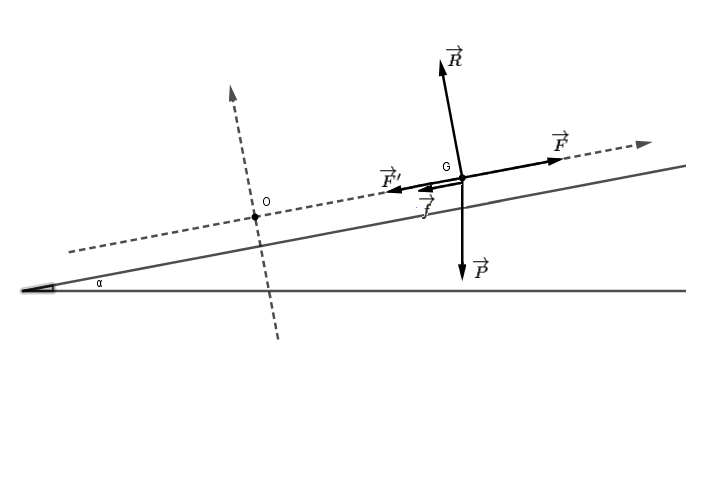
C'est bien ça.
Si on utilise les notations de l'énoncé :
F = M*g*sin(α) + F' + f

C'est en effet terminé en ce qui concerne le système "voiture".
Conformément aux instructions de l'énoncé il te faut maintenant répéter le même  travail en ce qui concerne le système "caravane"

L'application numérique se fera ultérieurement.
Pour l'instant il faut faire pour la caravane ce qui a été fait pour la voiture :
- Recherches des forces qui s'exercent. (combien y en a t'il ? quelles sont elles ? )
- Représentation sur un schéma de ces forces en respectant les notations imposées par l'énoncé.
- Application du principe d'inertie.
- Projection de la relation vectorielle afin d'obtenir une relation algébrique.

Il y'a quatres forces (nulle , deux résistantes, et une motrice)
_ la réaction

_ Le poids P et la force de frottement
_ la force motrice F'

P+F'+R+f'=0
Suivant l'axe xx':
Psin+ f'= F'

Voici le schéma

** image supprimée **

Attention les notations P et R ont déjà été utilisées pour la voiture.
On désignera par P' le poids de la caravane et R' la réaction de la route
En revanche on peut conserver F' dans les deux cas puisque le module de la force exercée par la voiture sur la caravane est égal à celui de la force exercée par la caravane sur la voiture.

Compte tenu de ces considérations la relation cherchée concernant la caravane est :
F' = M' * g * sin(α) + f'

En combinant les deux relations obtenues et compte tenu que l'énoncé fournit les valeurs de M, M',  f , f' et sin(α) on trouve les valeurs de F et de F'
L'énoncé ne donne pas la valeur de " g " : on prend la valeur moyenne g = 9,8 N/kg

Ah je comprends on calcul F' en premier lieu puis on calcul F . Ou je me trompe

C'est en effet une possibilité.
Sinon, on peut calculer F en premier en éliminant F' entre les deux relations.
On obtient alors F = ( M + M' ) * g * sin(α) + f + f '

A l'application numérique ça m'a donné :
F: (800+1200)*9,8*sin(4,8)+200+100
F:2008.25 N

F':800*9,8*sin(4,8)+200
F':837,41 N

Une montée de pente 8% correspond à un angle α tel que  sin(α) 0,08

F = (800 + 1200) * 9,8 * 0,08 + 200 +100 = 1868N
Ce résultat est à arrondir avec un nombre correct de chiffres significatifs

Merci beaucoup pour votre aide précieuse