Inscription / Connexion Nouveau Sujet
travail d'un ressort
bonjour jaimerais que vous m'expliquer
On dispose de deux ressorts R1 et R2 de masse négligeable,de longueur a vide lo=1cm de raideur k=16n/m
1 les deux ressort ont relies ensemble en un point G et tendu entre deux points fixes M et N. a l'equilibre leur commune longueur est L1=L2=20cm
(G se trouve en o origine du repere). calculer la tension de chaque ressort.
2)un operateur deplace le point G de O vers N de x.
a) etudier le nouvel etat d'equilibre du point G et exprimer l'intensité de la force F exercée par l'operateur sur G en fonction de K et x.
b) exprimer le travail de F de O vers G. faire l'application numerique pour x=2
c) calculer la puissance developpée par la force F sachant que l'operation dure 0.6s.
c'est tous ce que j'ai trouvé comme figure. merci de m'aider.
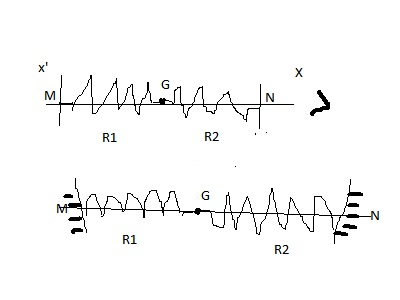
Bonjour,
Quelle est la longeur à vide des ressorts ?
L0 = 1 cm ou 10 cm ?
L'unité de force, le newton, a pour symbole N et non pas n
Donc la raideur d'un ressort s'exprime en N.m-1
À la question 2b :
x = 2 quoi ? 2 cm ?
En physique un résultat ou une valeur sans l'unité qui lui est nécessaire ne veut plus rien dire.

vu qu'il ont les memes valeurs de K Lo et L.
alors jai fait T=k(L-Lo)=16(20-15)=80N (mais je crois que ce serait trop facile comme sa)
Je ne vois pas pourquoi cela ne pourrait pas être facile...
__________
Le calcul est faux pour deux raisons :
. La raideur k est exprimée dans l'unité SI : le newton par mètre (symbole N.m-1 ou N/m) ; donc il faut que les longueurs et allongements soient exprimés en mètre pour calculer une force en newton
. Je ne vois pas d'où sort 15...

ok La raideur k est exprimée dans l'unité SI : le newton par mètre (symbole N.m-1 ou N/m) ; les longueurs et allongements soient exprimés en mètre pour calculer une force en newton
la longueur des ressorts a vide est Lo=15cm (erreur: cété pas 10cm)
donc T=k(L-Lo)=16(20-15)=80N

Tu ne lis pas ce que l'on t'écrit...
Il faut convertir longueurs et allongements en mètre !
________
D'ailleurs, je pense que si tu lisais tu n'oserais pas écrire "cété pas", mais tu écrirais "ce n'était pas"
C'est la dernière fois que je te rappelle que tu dois respecter la règle d'interdiction de l'écriture SMS.

Exact.
Question 2a
Que faut-il que fasse l'opérateur pour que le point G reste immobile ?
Quelles sont les nouvelles forces et les nouvelles intensités de ces forces ?

Ah oui. La physique n'est pas d'abord une question de formules.
Il faut d'abord réfléchir au phénomène étudié.
____________
Les deux ressorts sont identiques
Première question : ils sont tendus par des forces de même intensité ; ils ont les mêmes allongements ; le point G est au milieu de MN
Deuxième question : un opérateur déplace le point G de x = 2 cm
Que doit faire l'opérateur pour que le point G reste immobile ?
Quelles sont les forces en présence et leurs intensités ?

la seule chose qui me vient a l'esprit ce sont les barycentres (oups c'est mathematique sa!!!)
peut on le traduire en physique? je ne sais pas!
a ce que je comprend pour que G reste immobile. alors cette relation s'impose T((l-lo)+x)= F((lo-l)+x)
??
Pour que G reste immobile il faut que l'opérateur exerce une force.
Si l'opérateur lâche le point G, les ressorts vont se remettre dans la position de l'équilibre de la première question.
Donc il y a maintenant trois forces :
. la force du ressort 1
. la force du ressort 2
. la force exercée par l'opérateur
Quelle est la loi (ou le principe) que tu peux appliquer si l'ensemble est immobile ?
Donc tu peux calculer les intensités de ces trois forces
. elles ont même point d'application
. elles ont même direction (la droite MN)
. que valent les intensités et quels sont les trois sens de ces trois forces (de G vers ... )

si l'ensemble est immobile alors T1+T2+F=0 en vecteur
le sens de T1 est de G vers M
le sens de T2 est de G vers M
le sens de F est de G vers N
sur ce
T1= k(x-l)
T2= k(x+l)
F= 2kx
??
Expressions littérales incompréhensibles.
Le sens de T2 est faux.
Peux-tu calculer et donner les valeurs (valeurs numériques et unité) des trois forces ?

C'est à toi de les calculer.
Je t'aide en t'expliquant et en te montrant la méthode à suivre.
Mais je ne ferai pas le travail à ta place puisque je souhaite que tu progresses.

ok... on ne connait pas x
T1=kx = 35(20+x-15)= 175+35x
T2=kx = 35(20-15-x)= 175-35x
on demande d'exprimer F en fonction de k et x
F= k(20+x-15-20+15+x)= 2kx
??

On dispose de deux ressorts R1 et R2 de masse négligeable,de longueur a vide lo=1cm de raideur k=16n/m

Je ne crois pas.
Il faut relire ce que je t'ai écrit hier à 18 h 51
Puis, calculer les nouvelles longueurs des deux ressorts
En déduire les forces exercées par ces ressorts
Et en déduire la troisième force nécessaire, qui est exercée par l'opérateur

voila ce que j'ai établi :
si l'ensemble des forces appliqués sur G est immobile, alors T1+T2+F=0 en vecteur
leurs longueurs au debut était L1=L2=20cm
leurs nouvelles longueurs sont:
pour R1= (L1+x)
pour R2= (L2-x)
.donc l'allongement des ressorts sera:
pour R1= (L1+x)-lo
pour R2= (L2-x)-lo
sur ce apres projection sur x'x on a
-T1+T2+F=0  F= T1-T2
F= T1-T2
F= T1-T2
= k((L1+x)-lo)-k((L2-x)-lo)
F = 2k(x-lo)
??

Longueur à vide de chaque ressort l0 = 15 cm
Longueur des ressorts reliés entre eux, sans intervention de l'opérateur : L1 = L2 = 20 cm
Que valent les tensions des ressorts dans cette première position ? (direction, sens, valeur numérique et unité) ?

les tensions des ressorts dans cette première position valent
T1=T2= K(L-lo)= 16(20-15)= 80N
meme direction pour T1 et T2 : la droite (MN)
pour T1, sens : de G vers M
pour T2, sens : de G vers N
??
Les intensités des forces sont fausses.
Relis ce que je t'ai déjà écrit deux fois (le 10 janvier à 7 h 41 et à 15 h 44)

C'est exact.
Un opérateur déplace le point G de 2 cm vers le point N
Dans cet ordre :
. Quelle est la nouvelle longueur du ressort 1 ?
. Quelle est la nouvelle force exercée par ce ressort 1 ?
. Quelle est la nouvelle longueur du ressort 2 ?
. Quelle est la nouvelle force exercée par ce ressort 2 ?
. Quelle doit être l'intensité de la force exercée par l'opérateur ?

la nouvelle longueur du ressort 1 est L= 22cm= 0.22m
la nouvelle force exercée par ce ressort 1 est T1= 16(0.22-0.15)= 1.12N
la nouvelle longueur du ressort 2 : L=18cm= 0.18m
la nouvelle force exercée par ce ressort 2 est T2= 16(0.18-0.15)= 0.48N
a ce que je comprend pour une deplacement de 2cm
donc F=T2=0.48N
??
Oui pour les deux nouvelles longueurs des ressorts.
Oui pour les deux nouvelles forces exercées par les ressorts.
Non pour la force exercée par l'opérateur.
Puisque l'opérateur maintient le point G immobile, quelle loi (ou principe) peux-tu appliquer qui te permet de calculer la force exercée par l'opérateur ?

si on applique le principe de l'inertie, on aura:
T1+T2+F=0 en vecteur
apres projection on aura: F= T1-T2
= 1.12-0.48
= 0.64N
??
Oui, c'est bien l'intensité de la force exercée par l'opérateur pour maintenir en place le point G après l'avoir déplacé de sa position d'équilibre de 2 centimètres.
Il y a différentes manières de continuer.
Je te conseille de considérer l'énergie élastique de chaque ressort dans la position d'équilibre puis dans la position imposée par l'opérateur.
Mais on peut faire autrement.

je vois...
mais j'ai pas encore fait ce cours.
je connais pas ce que c'est l'energie elastique pour le moment; mais merci de me le preciser. sa me servira plus tard.
tu peut m'expliquer les autres manieres de resoudre ce probleme?
Une autre manière consiste à intégrer les travaux élémentaires. Mais ce n'est pas à ton programme en mathématiques.
C'est pour cela que je t'ai conseillé de considérer les énergies élastiques des ressorts.

Je suppose que si tu as cet exercice à faire c'est que tu peux calculer l'énergie élastique des ressorts...

mais oui je connais cette formule, mais sous le nom de travail de la tention du ressort.
donc j'applique cette formule, pour x=2cm ??
Oui, mais ne confonds pas ce x = 2 cm qui est le déplacement par rapport à la position d'équilibre avec le x que j'ai écrit à 17 h 27 et qui indique l'allongement !

Tout simplement parce qu'à la position d'équilibre (quand G est en O) les ressorts sont déjà allongés !



