Inscription / Connexion Nouveau Sujet
Théorème du centre d'inertie
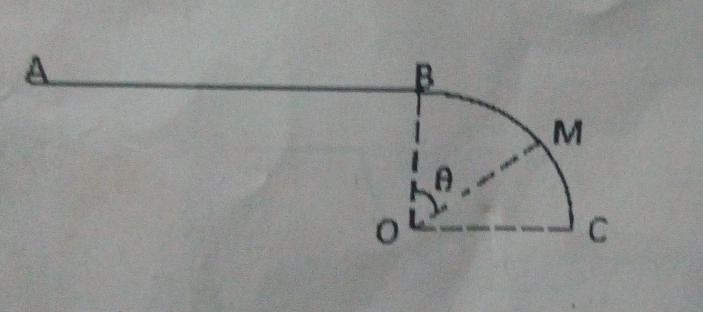
Un mobile de masse m : 1kg est lancé à t =0s d'un point A avec une vitesse Vo. La première partie du trajet se déroule sur un rail horizontal de longueurAB = l = 2m. Au cours de cette phase le mobile est soumis à une force de frottement constante f . En B le mobile aborde un rail à profil circulaire (de centre O) de rayon r=5m. Au cours de cette phase on
néglige tout frottement.
1.) a)Exprimer en fonction de Vo, l, m et f la vitesse du mobile en B.
b)-Calculer VB sachant que Vo = 10m.\s et f =20N.
2.) Exprimer en fonction de Vo, VB, f et m la durée du trajet AB. Calculer t1.
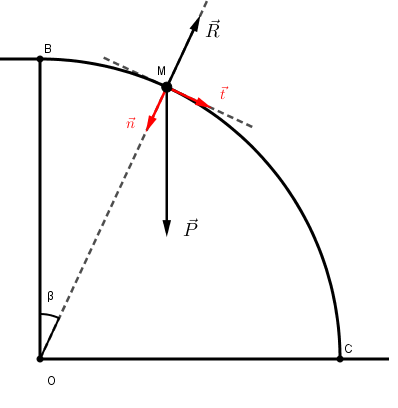
3.) Le point M est repéré par l'angle β= , Donner l'expression de la réaction R exercée par le rail sur le mobile en M en fonction de, β, m, g, r et VM( vitesse du mobile au point M )
4) a)Etablir l'expression de VM en fonction de VB, r, g et β.
b) En déduire l'expression de R en fonction de VB, r, g, β et m.
5.) Montrer que le solide quitte la piste en un point D.
Calculer l'angle β = . Prendre g =10 m.s-2
1)a) applican le théorème de l'énergie cinétique j'ai calculé VB=
b)
2.a je sais pas comment trouver la durée du trajet
Bonsoir,
Question 1.a) OK
Question 1.b) Ton résultat est invraisemblable. Tu trouves une vitesse en B presque 10 fois plus grande qu'en A alors qu'entre ces deux points le mobile n'est soumis à aucune force motrice et qu'il est au contraire freiné.
Question 2 : Toutes les forces qui s'exercent sur le mobile sont constantes. Leur résultante est donc constante ce qui implique que le mouvement est uniformément varié.
Applique la loi concernant la vitesse d'un mouvement uniformément varié : Tu obtiendra une relation entre V0 , VB et l'accélération " a " du mouvement.
Remplace " a " par son expression obtenue à partir de la 2e loi de Newton et tu auras la réponse à la question posée.
2.a) la duré du trajet AB
En appliquant le théorème du centre d'inertie j'aurais =m
En projetant dans le repère (o i j) sur l'axe (ox)
-f=ma => a==0.1m/s
On n'a a=0.1m/s2
x=1/2at2+Vot+x0
Or x0=0
=>1/2at2+Vot-x=0
AN: 0.05t2+10t-2=0
J'aurais deux solution dont t1=0.2
Du coup je ne sais pas comment exprimer la vitesse en fonction de Vo ; f VB
Pour la vitesse au point B je calcule sans avoir mis la racine carré
VB=9.96 m/s
Pense toujours à regarder la vraisemblance de tes résultats :
Tu avais trouvé une vitesse en presque 10 fois plus grande qu'en A ce qui n'était pas possible.
Cette fois tu trouves que la vitesse est passée de 10m/s à 9,96m/s donc qu'elle a diminué de seulement 0,4% ce qui est peu vraisemblable.
Donne le détail de ton calcul pour situer la nature du problème.
2.Exprimer en fonction de Vo, VB, f et m la durée du trajet AB.
Pouvez vous m'aider là j'ai pu calculer t1
Mais je ne sais pas comment Exprimer en fonction de Vo, VB, f et m la durée du trajet AB.
Pour l'instant je n'en suis pas à la question 2.
Il faut trouver la valeur numérique de la question 1.a)
donc calculer la valeur de VB à partir des valeurs de V0 , f, l et m
Cette fois ci c'est bon !
On pourra retenir aussi ( pour la suite ) que (VB)² = 20 (m/s)²
Question 2 :
Dans un mouvement rectiligne uniformément varié la vitesse dépend du temps selon la relation V(t) = V0 + a*t
A la date t=t1 on a V(t)=VB
On peut donc exprimer t1 en fonction de V0, VB , f et m puisque comme tu l'as indiqué dans ton post du 16-12-18 à 07:26 :
a = -f / m
2.t=
t1=0.27 s
3)en applican le théorème du centre d'inertie au point M et en projetant dans la base de frenet sur l'axe des j'aurais R=
4)a)en applican le théorème de l'énergie cinétique entre B et M j'aurais
b)R=
5)je ne sais pas quel est ce point D
Question 2 :
J'ai trouvé t1 = 0,28s
Question 3 :
Je ne trouve pas ( au signe près ) les mêmes résultats que toi :
2e loi de Newton :
Projection sur le repère de Frenet :
Question 4a):
On voit du premier coup d'oeil que ton résultat est faux car on ne peut pas avoir sous la racine la somme de deux grandeurs de natures différentes ( g et (VB)² )
Ces deux derniers résultats sont exacts.
Une suggestion pour le futur:
Si tu lances, presque en même temps, deux topics concernant un même thème pense à leur donner des noms différents pour limiter les risques de confusion.
Ici par exemple tu aurais pu, au minimum, intituler un topic "théorème du centre d'inertie 1" et l'autre "théorème du centre d'inertie 2"
D'accord je ferait cela la prochaine fois
Pour la question 3 je ne sais pas où dois je prendre le D
Ou bien c'est une erreur de l'énoncé
Ou bien il veulle dire C
Je suppose que tu évoques la question 5 et non la question 3
L'énoncé définit le point D comme celui ou le solide quitte la piste.
Sa position est pour l'instant inconnue.
Le but de cette question est précisément de trouver cette position en déterminant la valeur de l'angle
Indice : Que devient R au point D ?


