Inscription / Connexion Nouveau Sujet
Théorème de l’énergie cinétique
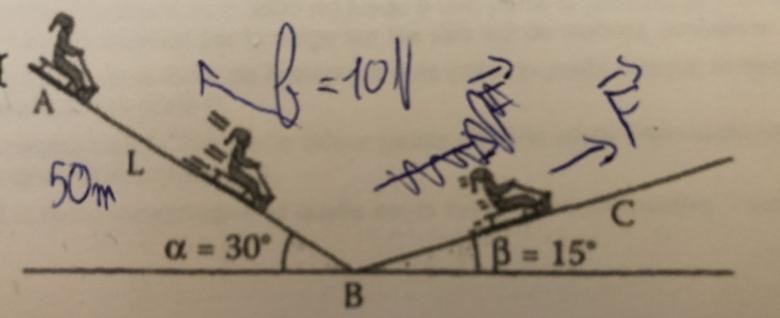
Bonjour voilà l'énoncé : Aux sports d'hiver, un enfant sur une luge part, sans vitesse, du somment A d'une pente de lonqueur L = 50,0 m inclinée de a =30degree sur l'horizontale. Au bas de cette pente (point B), il aborde une autre pente inclinée de l'angle B = 15degree sur l'horizontale. Il arrive alors au point C où la luge s'arrête. On supposera que les forces de frottement ont pour intensité f = 10 N et que la cassure de la pente au point B de la trajectoire ne modifie pas la valeur de la vitesse atteinte en ce point. Données : masse du lugeur m = 40,0 kg ; g = 9,81 N.kg'.
Je suis bloqué aux questions 5 et 6 qui sont:
5. Appliquer le théorème de l'énergie cinétique dans la phase ascendante (entre B et C), pour établir une relation entre le travail des forces appliquées au système et la variation de l'énergie cinétique lors de ce déplacement.
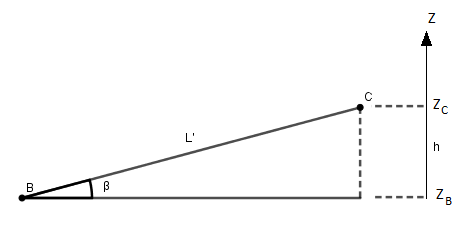
6. En déduire la distance L' parcourue par le lugeur avant de s'arrêter en C.
Je ne comprends pas comment trouver le travail des forces sur la remontée car nous ne connaissons pas la distance BC. Si quelqu'un pourrait me donner une piste ça m'aiderait beaucoup. Voilà mes réponses précédentes qui peuvent aider pour celle-ci :
DeltaEc(AB)= 9310J
v(B)=21,575m/s
Voici un schéma pour que ce soit plus clair:
Bonjour,
Je te souhaite tout d'abord la bienvenue sur le forum.
Il recopier intégralement ton énoncé d'exercice et proposer tes pistes de réflexion pour les questions déjà faites.
Tu as une fiche qui peut t'aider à démarrer (clique sur la maison) : 
[lien]
Voilà les questions précédentes:
1. Donner les caractéristiques (tableau) des différentes forces qui s'exercent sur le lugeur lors de la descente.
2. Donner les expressions littérales et calculer le travail de chacune de ces forces lors de la descente.
3. Calculer l'énergie cinétique du lugeur en bas de la piste (point B) en appliquant le théorème de l'énergie cinétique. 4. Calculer la vitesse du skieur en bas de la piste.
Pour trouver deltaEc(AB), j'ai préalablement calculé le travail des forces sur le système lors du déplacement de A vers B puis j'ai appliqué le théorème de l'énergie cinétique. Pour trouver la vitesse atteinte au point B, j'ai simplement repris la valeur de l'énergie cinétique et j'ai transformer la formule Ec=1/2*m*v^2.
Pour la question 5, j'ai essayé de calculer le travail des forces en fonction de la variable longueur que j'ai appelé x, c'est à dire que par exemple pour Wbc(Vitesse initiale) j'ai fais:
Wbc(vitesse initiale)=9310*x*cos(0)=9310x J
Pour les autres forces j'ai obtenu :
Wbc(P)=-101,560x J
Wbc(R)=0x J
Wbc(f)=-10x J
Je déduis ensuite que deltaEc(BC) vaut -9310 J car l'énoncé dis que le lugeur finit à l'arrêt en C, donc avec une énergie cinétique nulle, et que son énergie en B est de 9310 J.
J'applique ensuite le théorème de l'énergie cinétique et voilà mes calculs :
-9310=9310x-101,560x-10x
Je trouve x ≈ -1 m . Ce résultat est évidemment faux car il ne va pas s'arrêter à -1m mais je ne comprends pas ou j'ai pu faire une erreur, je pense donc que j'étais sur la fausse piste depuis le départ.
Bonsoir,
Wbc(vitesse initiale)=9310*x*cos(0)=9310x J
Je ne comprends pas trop cette égalité.
On a l'impression que tu considères que la vitesse initiale serait une force dont tu chercherais à calculer le travail.
3 forces s'exercent sur l'enfant lors de son trajet entre B et C
a) Son poids
b) La réaction normale
c) La force
Question 5 :
Soit ΔEc la variation d'énergie cinétique du système {Enfant + Luge} sur le déplacement BC
Le théorème de l'énergie cinétique permet d'écrire que :
Question 6 :
L'énoncé impose de noter " L " la distance entre A et B. Il n'y a donc aucune raison d'utiliser " x " à la place de " L' "
L'égalité obtenue en réponse de la question 5 donne :
Et puisque VC=0 :
Je te laisse terminer.
Question 6 :
Attention à ma faute de frappe :
J'ai écrit : L'énoncé impose de noter " L " la distance entre A et B.
J'aurais du écrire : L'énoncé impose de noter " L' " la distance entre A et B.
Merci pour votre aide, en effet je pensais que la vitesse initiale était une force, j'essayais donc de trouver son travail. Je vais continuer l'exercice et si je rencontre à nouveau des problèmes je reviendrais écrire ici. Bonne journée !
J'ai oublié de préciser mais je pense que vous vous êtes trompé sur la formule pour calculer le travail d'une force, il faut utiliser cos(...) et non sin(...).
Autant pour moi, j'ai transformé la formule différemment de vous donc l'utilisation du cosinus reste juste dans la mienne :
Je ne calcule pas DeltaEc car j'ai déjà déduis qu'elle vaut -9310 J
L'idéal est de poursuivre le calcul littéral avant toute application numérique :
En partant de :
On obtient L' = .........................
et on passe ensuite à l'application numérique
1/2*m*Vb^2=m*g*L'*sin(teta)+f*L'
(1/2*m*Vb^2)/2L'=m*g*sin(teta)+f
J'effectue un produit en croix:
2L'=(1/2*m*Vb^2)/(m*g*sin(teta)+f)
L'=1/2((1/2*m*Vb^2)/(m*g*sin(teta)+f))
Une fois remplacé par les valeurs, j'obtiens 41,726 au lieu de 83,45 soit la moitié, je pense donc que j'ai fait une erreur mais je ne sais où ...
Bonsoir à vous deux,
@ ghost57455 : profite de la période estivale pour t'approprier les outils du site pour écrire des formules, ce sera beaucoup plus lisible pour nous tous (clique sur le raccourci ci-dessous) :
extrait de 
la FAQ du forum :Q10 - Puis-je insérer des symboles mathématiques afin de faciliter la lecture de mon message ?
guide latex
présent sous la zone de saisie du message. La liste complète des caractères mathématiques est disponible dans le 
mode d'emploi du forum1/2*m*Vb^2=m*g*L'*sin(teta)+f*L'
(1/2*m*Vb^2)/2L'=m*g*sin(teta)+f L'erreur est dans cette ligne
J'effectue un produit en croix:
J'ai trouvé mon erreur, pour supprimer les L' d'un côté j'avais seulement à diviser par L' et non pas part 2L'.
La formule est donc:
J'obtiens le même résultat que mes calculs précédents à savoir 83,45m la formule est donc juste.
L'exercice est finit, merci pour votre aide !
Annuler
connectez vous