Inscription / Connexion Nouveau Sujet
Tension / Force avec fils
Bonjour,
j'ai un problème avec un exercice de physique qui me dit: " Détermine par calcul la tension de chaque fil dans les trois cas suivants:..."
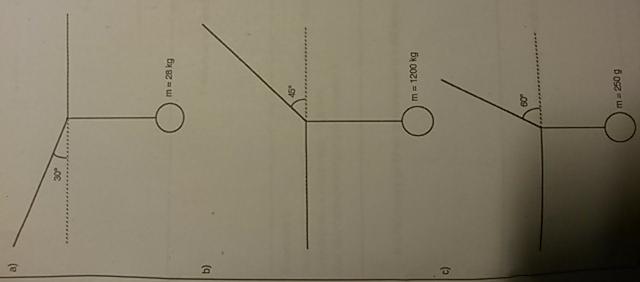
Le poids est attacher à une corde qui est attachée à deux autres. (Voir Photo)
A) angle donné: 30
Masse de l'objet: m= 28kg
B) angle 45
Masse de l'objet: m= 1200kg
C) angle 60
Masse de l'objet: m = 250g
Pour le moment je ne comprends pas comment je pourrais les trouvées car je ne comprends pas bien la façons de le faire surtout que j'ai l'impression qui manque un angle afin de savoir la tension.
Merci pour votre aide.
Bonjour ,
on considère que le système est en équilibre et donc que la résultante des 3 tensions est nulle .
Mais la solution ne me semble pas du niveau 5°
Cordialement
Salut,
"Mais la solution ne me semble pas du niveau 5° "
Il est possible que ce soit 5eme Belgique ou Suisse ... qui correspond à une 1ere en France.
Aide pour le 1er :
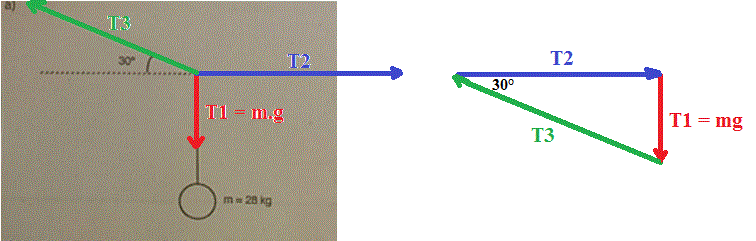
Comme il s'agit de cordes ... les tensions dans celles-ci ont forcément la direction des cordes.
T1 = m.g = 28*9,81 = 275 N (arrondi)
T1 = T3 * sin(30°) et donc T3 = ...
T2 =T3.cos(30°)) = ...
Sauf distraction. 
Intervenir à plusieurs risque d'embrouiller le demandeur qui ne s'est pas encore manifesté .
Donner la solution (même qu'en partie) n'est déjà pas terrible mais si elle est imprécise ...
Je ne pense pas que les forces représentées sur le schéma de J-P soient celles demandées (tension des fils)
"Je ne pense pas que les forces représentées sur le schéma de J-P soient celles demandées (tension des fils)"
Non ? peut-être comme on dit "par chez moi".

Bonjour,
Merci pour vos aides, si je n'ai pas pu me manifester c'est parce que j'avais cours toute la journée. Et pour l'exercice de 5eme en faite je viens de suisse et je chercher une correspondance avec la France ( je suis en la dernière année avant le lycée) et ce que je cherche avant tout pour cette exercice c'est la méthode. Merci beaucoup
"ce que je cherche avant tout pour cet exercice c'est la méthode"
Je te l'ai donnée dans mon premier message.
La tension dans une corde tendue a toujours la direction de la corde (ce ne serait pas obligatoirement vrai avec des barres rigides à la place des cordes).
Donc au point de rencontre des 3 cordes, les efforts faits par celles-ci (au niveau du noeud) ont les direction que j'ai indiquées sur mon dessin.
Pour les sens des forces, c'est évident ... une corde ne peut pas pousser mais seulement tirer sur un point fixe. (réfléchis 1 s et ce sera évident pour toi).
Comme le "noeud" est immobile, la somme vectorielle des 3 forces (qui sont les tensions dans les cordes) appliquée au noeud est nulle.
Donc, en mettant les vecteurs représentant les 3 forces "bout à bout", on obtient un triangle fermé.
Dans ce triangle, les directions des cotés sont celles des cordes ... donc on connait les angles de ce triangle.
Si on connaît l'amplitude d'une seule des 3 forces ... on peut donc calculer les 2 autres (par les propriétés du triangle).
Or, il est facile ici de calculer l'amplitude de T1.
Cette corde est "tendue" par le poids de la masse m ... et donc T1 = mg.
Sauf distraction.

Ce n'est pas tout à fait ma vision des choses . Je m'explique : si la corde sur laquelle est attaché la masse était élastique (un ressort par exemple) et qu'on enlève le poids , quelle force ferait remonter le ressort si ce n'est sa tension (proportionnelle à l'allongement)
L'approche recommandée est la suivante :
Le point A est soumis à la force =m g . Comme il est en équilibre , une force
opposée à
lui est aussi appliquée .
est la tension du fil avec
= -
De même le point B (en équilibre) est soumis au poids et aux tensions des fils
et
avec :
+
+
= 0 ou
+
= -
Il reste à calculer |t1| et |t2| en s'aidant d'un peu de trigo .
Remarque complémentaire : et
sont la décomposition de
ou
=
+
Pas tout à fait d'accord sur les objections à mon approche.
La tension dans un fil n'a pas de "sens".
La tension ne "s'applique" nulle part.
C'est un scalaire qui donne la valeur de la force qu'il faudrait exercer sur les deux extrémités du fil qu'on couperait pour les garder en contact.
Je suis d'accord que le fil 1 tire le poids vers le haut ... mais il tire aussi le point B vers le bas.
Et dans les 2 cas, c'est la tension du fil qui provoque ces effets.
La tension T1 (qui est un scalaire) du fil vertical a 2 effets :
- Elle provoque une force verticale vers le haut et d'amplitude T sur la masse m
- Elle provoque une force verticale vers le bas et d'amplitude T sur le "noeud" B.
Elle peut aussi être calculée pour évaluer la contrainte dans le fil (de nouveau en scalaire = T/S avec S la section du fil)
C'est plus compliqué évidemment dans les cas de fil pesant.
Ceci étant dit, on peut donc calculer les 3 SCALAIRES que sont T1, T2 et T3 comme je l'ai fait dans mon message... Qui tient compte des 3 forces (en direction et sens) exercées par les 3 fils en B
Sur mon dessin, par exemple, la force (dont grandeur vectorielle) exercée en B par le fil vertical est verticale (direction du fil), est vers le haut (puisque le fil est tendu) et à pour amplitude T1 (qui est un scalaire).
Même raisonnement pour les autres forces.

Notre divergence ne porte que sur t1 et sur le fait que la tension d'un fil à un sens qui est opposé à une force qui lui est appliqué . Sans force appliquée à un fil , pas de tension .
En B , c'est P qui crée les tensions t2 et t3 .
Certes, il n'empêche que par définition, la tension dans un fil est un SCALAIRE.
"le fait que la tension d'un fil à un sens qui est opposé à une force qui lui est appliqué ."
Pas du tout d'accord avec cette formulation.
La tension du fil est un SCALAIRE et une force est grandeur VECTORIELLE.
Il n'est pas question de comparer les directions et sens d'un vecteur et d'un scalaire.
La tension (scalaire) dans un fil tendu rectiligne non pesant est imposée bien entendu par les forces (grandeurs vectorielles) sur les 2 extrémités du fil ... mais on ne peut pas identifier la tension et les forces (qui sont de natures différentes (scalaire ou grandeur vectorielle)).
Parler du sens (ou de la direction) d'une tension dans un fil n'a aucune signification (c'est confondre tension (scalaire) avec force (grandeur vectorielle)).
En B , c'est P qui crée les tensions t2 et t3 .
Oui, et alors ? C'est aussi dépendant des différentes positions d'attaches et des longueurs des fils 2 et 3 (donc de la géométrie de l'essai).
Les tensions dans les différents fils sont imposées par la géométrie de "l'essai" et par la valeur de P.
Et ces tensions sont "reliées" aux 3 forces que j'ai représenté en B sur mon dessin.
Les directions et sens de ces forces (celle de mon dessin) sont imposées par la géométrie et leurs amplitudes (seulement l'amplitude et rien d'autre) ont les mêmes mesures que les tensions dans le fil (qui sont des SCALAIRES).

La confusion vient du fait que T1 , T2 et T3 (supposés être des tensions donc scalaires) sont représentés par des vecteurs .
Si on garde T pour les tensions , alors T1 = |P| et on ne représente pas T1 par un vecteur .
La confusion vient du fait que T1 , T2 et T3 (supposés être des tensions donc scalaires) sont représentés par des vecteurs .
Pas chez moi, note que sur mon dessin, il n'y a aucune flèche sur les notations T1, T2 et T3
Ce sont donc des scalaires représentant les normes des forces dont les directions et les sens sont évidents sur le dessin (par les flèches sur le dessin).
Je pense qu'il n'y a aucune incohérence dans ce que j'ai fait ... à condition bien entendu d'utiliser les conventions que j'ai décrites tout au long de ce topic (et qui sont très largement utilisées)



