Inscription / Connexion Nouveau Sujet
Suivi cinétique par spéctrophotométrie
Voici l'énoncé:
On étudie la cinétique de décomposition de l'eau oxygénée H2O2(aq) par les ions iodure I-(aq) en présence d'acide sulfurique. L'équation de la réaction s'écrit:
H2O2(aq) + 2H3O+(aq) + 2I-(aq) --> 4H2O(l) + I2(aq)
On suit l'évolution du système par spéctrophotométrie. L'absorbance A est liée à la concentration en diiode [I2] (substance colorée du milieu réactionnel) par une relation que l'on établira.
I/ Etude préliminaire:
On mesure l'absorbance A pour des solutions de diiode I2(aq) de concentrations connues. On obtient alors les mesures suivantes:
[I2] (mol.L-1) | 0 | 0,0001 | 0,0005 | 0,0010 | 0,0020 | 0,0040 | 0,0060 | 0,0080 |
A | 0 | 0,037 | 0,102 | 0,203 | 0,304 | 0,741 | 1,073 | 1,550 |
1. Tracer la courbe de l'absorbance A en fonction de [I2] échelle : ordonnée, 1cm pour 0,1 unité d'absorbance, abscisse, 1cm pour 1.10-3 mol/L
2. Par une méthode graphique, exprimer la relation liant l'absorbance A à la concentration de diiode [I2], en indiquant le calcul effectué.
II/ Conditions expérimentales:
On place dans la cuve de mesure du spéctrophotométre un volume V0=1,0mL de solution d'eau oxygénée, de concentration initiale C0=0,080mol/L. A l'instant t=0, on ajoute un volume V'0=1,0mL de solution acidifiée d'iodure de potassium, K+(aq)+I-(aq) de concentration C'0=0.060 mol/L
1. Quel est le réactif qui limite cette réaction ? Justifier votre réponse.
2. Calculer la valeur de la concentration en diiode en fin de réaction.
III/ Etude cinétique:
On lance la mesure de l'absorbance en fonction du temps en effectuant une mesure toutes les secondes. On obtient l'enregistrement reproduit sur la figure suivante.
(Voir image ou cliquez sur le lien)
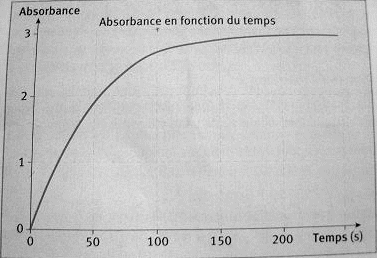
1. Exprimer la vitesse de réaction en fonction [I2] à un instant t, puis en fonction de l'absorbance A de la solution à un instant t.
2. Les vitesses de réaction aux instants t =10s et t =150s ont pour valeurs respectives v(10s) = 2,5.10-4 mol/L/s et v(150s) = 5.10-6 mol/L/s.
Comment évolue la vitesse de réaction au cours du temps? Donner une explication de ce phénomène.
Bonsoir,
J'ai commencé par tracer mon graphe et logiquement on obtient une droite passant par l'origine ce qui m'a permis d'en déduire une situation de proportionnalité entre l'absorbance et la concentration, donc d'une relation A = k*[I2].
Après on doit utiliser deux points de la droite pour calculer le coefficient directeur de la droite k, pour obtenir le coefficient de proportionnalité.
logiquement on devrais trouver quelque chose aux alentours de k=0.005
Mais j'en suis pas très sur... ^^'
Pour le II/ je sais qu'il faut faire un tableau d'avancement mais j'aimerais savoir qu'entendent-ils par "Justifier votre réponse" ? =/
Pour la suite je pense que je vais bloquer un peu j'ai du mal à voir les expressions recherchés..
Merci d'avance pour votre aide. =)
Edit Coll : image placée sur le serveur de l'  Merci d'en faire autant la prochaine fois !
Merci d'en faire autant la prochaine fois ! 
![]() [lien]
[lien]
justifier le choix du réactif limitant consite à calculer le xmax à partir du tableau d'avancement.
les données te permettent de calculer les quantités initiales en H2O2 et I-.
Ce xmax te permettra de trouver la quantité de I2 formé.
Pour calculer sa concentration:attention le volume de la solution a augmenté
Personne ne m'a répondu donc j'ai continué et je suis arrivé à ces résultats:
1. L'eau oxygéné est le réactif qui limite la réaction étant donné que: xmax = 8,00.10-5mol < xmax = 3,00.10-5
(suivant le tableau d'avancement)
2. n(I2) = 2*xmax
n(I2) = 1,60.10-4 mol
Vtotal = V'0 + V0 = 2,0 mL = 2,0.10-3 L
d'après n = C*V alors C(I2) = n(I2)/Vtotal = 8,00.10-2 mol.L-1
Je me suis rendu compte apres -_-
au final je trouve C(I2) = 1,5.10-3 mol.L-1
ça devrait être bon =)
Pour le III/ 1. je pense avoir trouvé mais je suis pas sur pouvez vous m'aider svp =)
je trouve:
v= d[I2]/dt mais pour A je n'y arrive pas =/
tu as écris que A=k[I2} donc [I2}=A/k k étant une constante
donc v=1/k*dA/dt.
Logiquement,en calculant la pente de la tangente au point d'abscisse t=150 et en divisant par la valeur de k (calculable sur le premier graphique) on devrait retrouver la vitesse indiquée dans l'énoncé
J'ai bien compris mais pour une bonne rédaction dite moi si c'est bon ou juste :
x = ni(I2)-n(I2)
v = 1/V * d(ni(I2)-n(I2))/dt
v = -1/V * d(n(I2))/dt
v = -d(n(I2)/V)/dt
v = -d[I2]/dt
et
A=k[I2] alors [I2]=A/k
donc v = -d(A/k)/dt
je ne vois pas l'intéret de x ,puisque cette variable n'est pas utilisée par la suite.
la 2ème expression est incorrecte.
par définition,la vitesse de formation d'un produit à un instant t est la limite de la variation de la concentration entre deux dates t2 et t1.Autrement dit,elle est égale à la dérivée par rapport au temps de la concentration molaire à cet instant.
d[I2]/dt = limite de [I2]2-[I2]1/t2-t1 quand t2-t1 tend vers 0
3ème expession n'est négativepourquoi v devient-il négatif?Il s'agit d'une vitesse de formation(>0)
la 4ème inutile
la 5ème avec[I2] n'est pas négative et suffirait comme réponse
je sortirais 1/k de la parenthèse.
v=1/k*d(A)/dt
Ok merci pour ton aide Coriolan =)
par contre une dernière chose c'est au sujet du phénomène qui se produit je vois pas vraiment comment expliquer ça =S
la vitesse de formation diminue au cours du temps(la pente des tangentes à la courbe diminue au cours du temps).Au cours du temps la quantité de réactifs diminue ,donc la probabilité des chocs efficaces entre les réactifs diminue ce qui entraîne un ralentissement de la formation de produits formés.


