Bonjour

1) Il y a bien le poids, la force de rappel du ressort et la réaction R du sol (n'est-ce pas la meme que la réaction normale d'après toi ???). Quelles sont leurs caractéristiques ?

2) oui très bien...sauf que R et RN c'est la meme force !!!

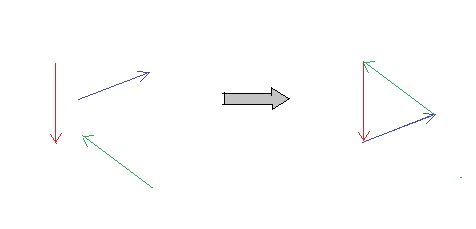
3) Fais d'abord un beau schéma de la situation en prenant comme échelle : 1cm = 3N et en tracant les angles au rapporteur. Ensuite il faut que tu additionnes les vecteurs tracés ! Pour cela tu prends par exemple le vecteur P et tu retraces à partir de sa pointe le vecteur R. Puisque tu as dis que P+R+T=0 on va donc former au final un triangle ! Tu n'as plus qu'à tracer T, à mesurer sa longueur et à en déduire la valeur de la force T !

Pour résumer je te donne un exemple avec 3 vecteurs quelconques :

Bonsoir! Merci de votre réponse! Je reprends donc...

1) Bilan des forces:
Poids P (P= m*g)
Réaction au support (R = Rn + Rt)
Tension (T = k*l ou T= m*g)

2) Je reprends la même chose en enlevant Rn de l'équation.

3)Alors la.. Je ne comprends pas tout...

Pour R: je prends quoi comme valeur? Malgré le principe d'inertie, P+R0 Donc la norme du vecR est différente de 3N ?

1) Quelles sont les caractéristiques de ces forces (direction, sens et norme) ?

Peux tu insérer ton schéma dans ton prochain message stp ? (Utilise pour cela l'icone "Img" situé en bas de l a fenetre de message)

d'accord..

Le poids:
dir: verticale
sens: vers le centre de la terre
norme: P = m*g
Point d'application: centre de gravité

La réaction au support:
dir: verticale
sens: opposée au centre de la Terre
norme: R= Rt+ Rn = Rn
pt: centre de la surface de contact

La tension:
dir: celle du ressort
sens 1: vers l'intérieur du ressort lorsque celui ci est étiré
sens 2: vers l'extérieur du ressort lorsque celui ci est comprimé
normes: T = k* ^L ou T = m*g
point d'application: point qui relie le ressort au système.

voila.. c"est juste? =)

Pour le schéma... je le fais comment? Sur paint? je ne peux pas expliquer comment je fais plutôt?

Pour le poids et la tension du ressort c'est juste ! En revanche pour la réaction du support non !

Excusez-moi...

dir: perpendiculaire a la piste
sens: vers le haut
norme: (sachant que Rt = 0 on a ) Rn = R ... non?
pt: centre de la surface de contact.

c'est mieux?

Voici mon premier schéma...

Le problème c'est qu'après avoir placé le poids, franchement, je ne sais comment placer la réaction au support... (c'est Rn, mais pour la norme?)

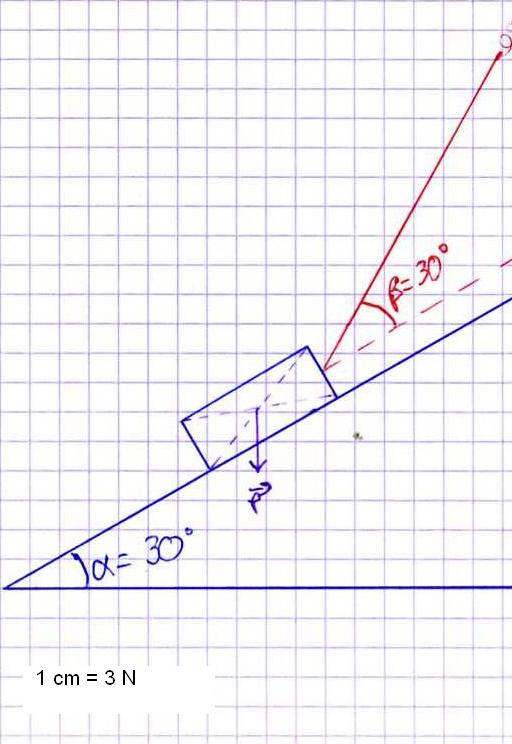
Au sommet de la fleche de P tu traces une droite perpendiculaire a la pente.  Tu prolonges la droite portant le vecteur T. Tes 2 droites se coupent en un point qui sera en fait la pointe du vecteur R.

J'ai prolongé les droites...

Voici ce que ca me donne.. Ca semble bon? (le vecteur T me semble vraiment petit . . . )

Mon schéma:

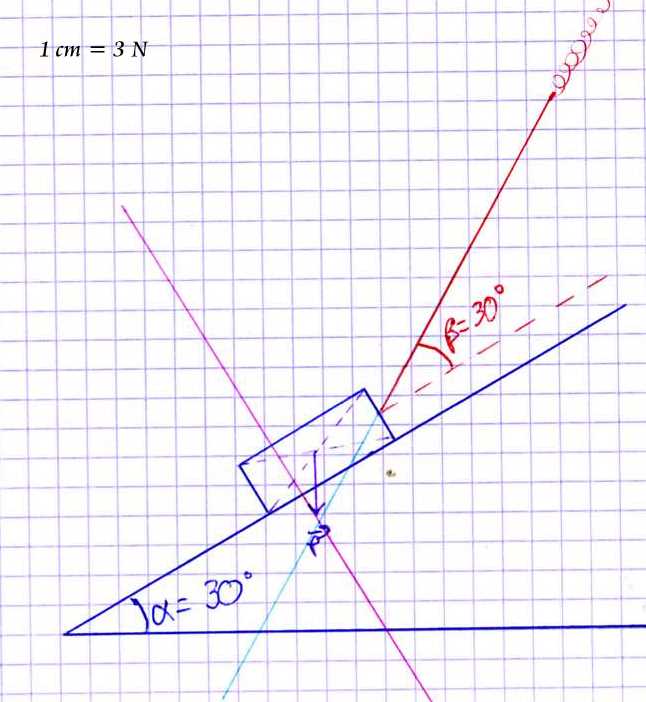
Pour la droite violette c'est bon mais pour la droite bleu-clair ce n'est pas à cet endroit que je voulais que tu l'as traces...

Garde en tete qu'il faut que les 3 vecteurs forment un triangle (car la somme de ces vecteurs est nulle) : voir schéma du message du 20-12-10 à 12:55

Donc il faut que la pointe du vecteur T rejoigne le centre de gravité O du solide (le point de départ du vecteur P) !



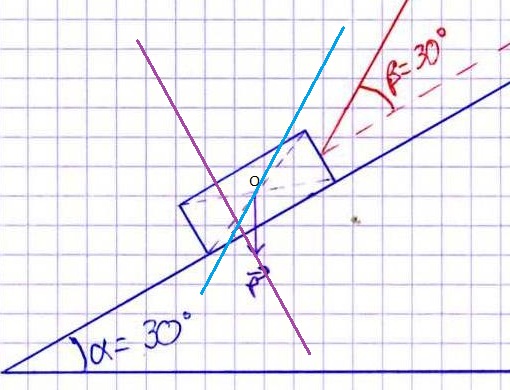
Ca forme bien un triangle !!

OK?

Ah d'accord... Désolé.

Je refais un schéma. (voir fin de message)

est-il juste?

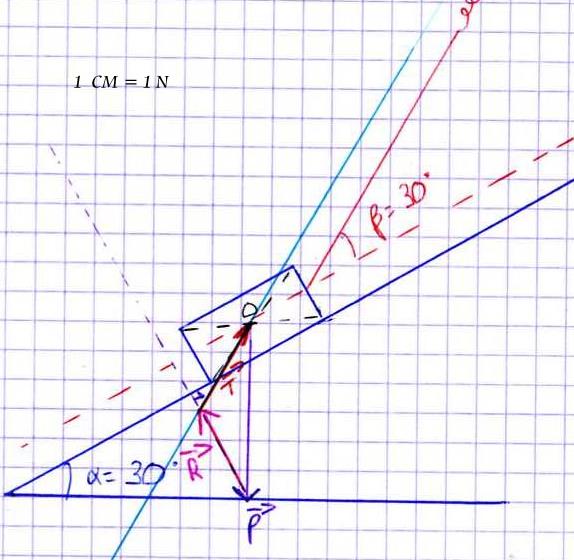
Voila! Tu as compris ! Mais attention de respecter ton echelle pour les longueurs! Je vois que tu as change...

Oui j'ai changé car on voyait mal pour 1 cm = 3N

Donc pour la question 3 : je présente cette représentation graphique et j'en déduis par lecture graphique que T 1.5 cm donc 1.5 N.
Ainsi, la force exercée par le ressort sur le mobile est de 1.5N

oui?

4) pour les axes, je peine à les placer et à n'oublier aucune partie de la démonstration... Je ferais ceci:

Je prends l'axe des abscisses sur T et l'axe des ordonnées sur P.
Je prends ||T|| = 1 pour l'axe des absicesses et || P || = 1 pour l'axe des ordonnées.

De là, pour la résolution analytique... je suis bloqué...

J'ai plutôt 1,8 N donc, je remplace 1,5 par 1,8 N...

3) attends quelle échelle as tu pris finalement ?

4) Voici les axes qu'il faut placer :



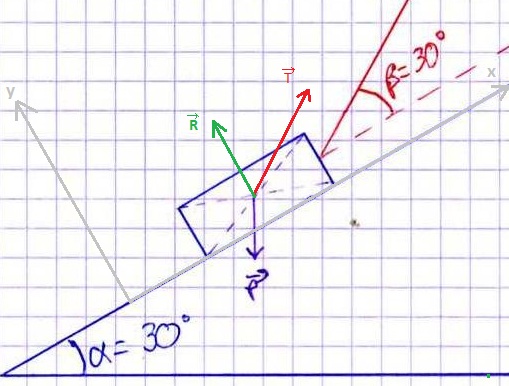
A toi de jouer maintenant !

J'ai pris 1 cm = 1N (c'est plus lisible que 1cm = 3N) c'est bon ou non?

4) Pourquoi ces axes en particulier?
Nous avons effectué une résolution analytique de ce genre en cours (que je n'ai pas comprise....) et mon professeur m'a fait placer des axes sur deux des vecteurs pour "supprimer des coordonnées" (selon lui)...

Je n'ai pas compris la méthode de résolution...

Ok donc 1cm 1N oui ca me va !

4)

Oui effectivement! c'est exactement ça...

Donc à partir de là, comment faire? Je dis les coordonnées des trois vecteurs par rapport à l'origine du repère?

Pour projeter un vecteur voici la méthode :



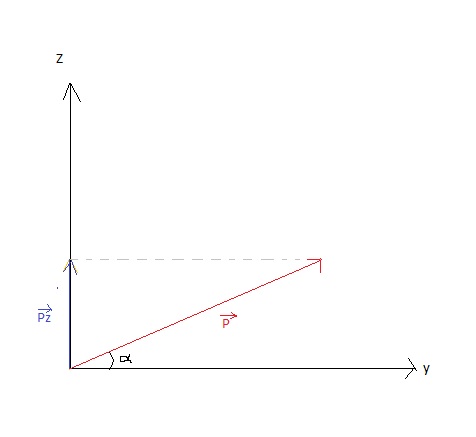
Ca donne donc ici : = sin

OK?

Tu n'as plus maintenant qu'à projeter les 3 vecteurs d'abord sur l'axe Ox puis ensuite sur l'axe Oy. Détaille bien tes calculs pour chaque cas !

D'accord... Je veux bien commencer juste pour T [c'est le seul demandé en fait...]  (et ressemblant à l'exemple).

On a: T (Xt; Yt)

On a: Xt = vectT * cos

On a: Yt = vectT * sin

... je pense...

Mais après, pour les calculs, ça se gâte.

On a: Xt = 1,8 * cos30 = 1.55
et: Yt = 1,8 * sin30 = 0.9

C'est faux, non?

Ah d'accord! Merci...

Donc en fait, je dis que:

T (Tx; Ty) + R (Rx; Ry) + P (Px; Py) = 0
T (Tx; Ty) = -R (Rx;Ry) - P (Px; Py)

non?

De plus, je ne comprends pas comment utiliser "T" danx Tx = T*cos par exemple...

oulah attends ! Pour ne pas s'embrouiller avec les coordonnées, écris plutot :

Sur l'axe Ox : Tx-Px+Rx=0
Sur l'axe Oy : Ty-Py+Ry=0

Ca donne quoi alors ?

D'accord.

Sur l'axe Ox on a: Tx- Px + Rx =0 donc Tx = Px - Rx
Sur l'axe Oy on a: Ty -Py + Ry =0 donc Ty = Py - Ry

Mais ensuite que fait-on..?

Remplace Px,Rx,Tx,Py,Ry et Ty par leur expression !

Px = P * cos30°
Py = P * sin30°

Rx = R * cos30°
Ry = R * sin30°

Tx = T* cos30°
Ty = T * sin30°

Non?

Il me semble que c'est :
Px = P*sin
Py = P*cos

Le vecteur R fait-il un angle avec l'axe Ox ? avec l'axe Oy ? Donc que valent Rx et Ry ?

Tx = T*cos oui !
Ty = T*sin oui !

Bonjour!

Arg, désolé pour P...

Pour T, c'est déjà ca!

Pour R...

R ne fait pas d'angle avec Oy, mais un angle de 90° avec Ox. non?

Tout a fait !

Donc en projetant le vecteur R sur Oy on obtient quoi (Ry vaut quoi?) ?
En projetant le vecteur R sur Ox on a donc : Rx=...?

Ry = 0 car cos 90° = 0

Rx = R non?

Et non ! C'est le contraire !

Lorsque tu projettes R sur l'axe Oy, le vecteur est confondu avec cet axe.
Lorsque tu projettes R sur l'axe Ox, le vecteur ne possède aucune composante suivant cet axe.
Donc Ry=R et Rx=0 !!!!

Ah mince...

A partir de là, on fait une équation?

Tx - Px + Rx = 0

donc Tx = Px - Rx
        = (P x sin) - 0
        = P x sin30°

(comment fait-on après?)
et

Ty -Py+ Ry = 0

donc Ty = Py - Ry
        = (P x cos)- R
(comment fait-on après?)

S'il vous plait, mon DM est pour demain...

Aidez-moi!

Me revoilou !

Je n'étais plus très dispo désolé !

Donc tu as obtenu une expression de Tx. Tu peux donc en déduire sa valeur.
Or on a dit que Tx=T*cos !
Donc ?

Meilleurs voeux =)

alors

Tx = T x cos et Tx = P * sin30

donc = > T *cos30 - (P * sin30)

Non?

oui mais ca ne nous avance pas beaucoup...

Tu sais que : T*cos=P*sin
Donc T=... c'est plus simple non ?

T = Psin30 / cos30
T = 3*sin30 / cos30
T = 3

?

oui voila : T=1,73N !! Tu avais trouvé 1,5 précédemment... bon peut etre des erreurs de lecture !

C'était 1,8 ! Je m'étais relu!

Par contre, pourquoi ne prend-on pas T y?

Parce que la, on ne prend que Tx non?

Oui mais si on prenait Ty on serait coincer par R que l'on ne connait pas...

Je t'ai fais projeter sur les 2 axes pour que l'on ait 2 équations. En les développant on a vu que seule celle issue des projections sur l'axe Ox pouvait etre exploitée (car elle ne comportait que des valeurs connues : P et l'angle !!!).

C'est un raisonnement classique mais efficace (enfin je pense) !!

OK?

Très bien, je comprends! =) Merci beaucoup!

Juste une question!

Pour la question 5

(en supposant que l'allongement du ressort soit de 3 cm, quelle est la constante de raideur de celui ci?)

> On a : T = 1.73N et l = 3 cm = 0.03 m

On a: K = T / l (vient de T = k * l)

Donc:

K = 1.73/ 0.03 ) 57,7 N/m

est-ce juste?

Tout a fait bravo !!

C'est bon pour l'ensemble de l'exo tu as bien compris ?
Il faut s'entrainer sur ce genre de truc ! Ce n'est pas compliqué mais il y a des réflexes à acquérir !

Bonne année et meilleurs voeux !!!

Merci beaucoup Lulu!

Par contre... On me met dans la question 4 : "Vus veillerez à rédiger correctement et à n'omettre aucune partie de la démonstration..."

Je la fais dans quel ordre?

Dans l'ordre dans lequel on l'a fait !!

- Dessine un beau schéma en projetant les vecteurs sur Ox et Oy.
- Donne les expression des projetés.
- Grace à la loi de Newton déduis-en Tx puis T !

D'accord, très bien =)

Je fais du zèle en écrivant P, R? ou non?

pardon ? no comprendo !

Pour Px, Py, Ry, Rx, je les écris même si ce n'est pas demandé?

mais oui bien sur !!!