Inscription / Connexion Nouveau Sujet
sortie de Bunker
Bonjour,
j'ai du mal à résoudre le problème de physique suivant :
II- Sortie de « bunker »
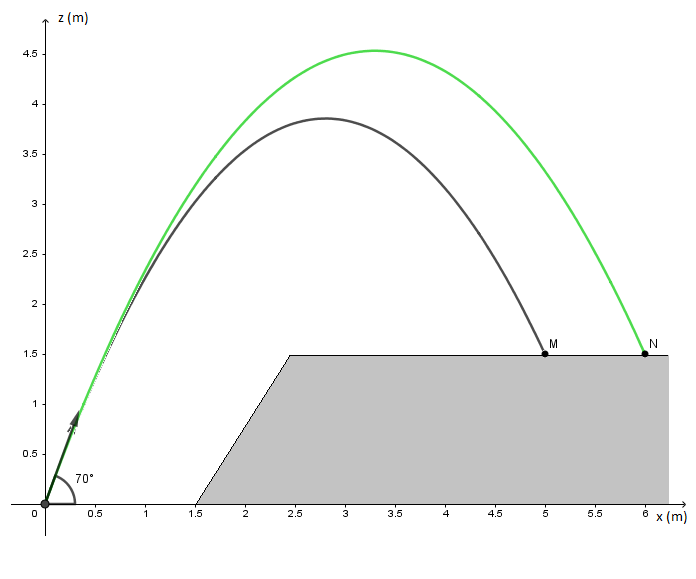
Le joueur de golf doit maintenant sortir sa balle d'un « bunker » de profondeur h = 1,5 m. Un « bunker » est un trou de sable près de la surface engazonnée. Le joueur utilise un « club » et communique à la balle une vitesse V0 faisant un angle α = 70° avec l'horizontale. À la date t = 0 la balle, supposée ponctuelle et de masse m = 45 g, part du point O. On considère le champ de pesanteur terrestre uniforme et on néglige les frottements de l'air sur la balle. Le vecteur g représente l'intensité de la pesanteur, sa valeur est g = 9,8 m.s-2. Le joueur veut envoyer sa balle entre les points M et N.
On prend comme origine des dates t = 0 s, le moment où la balle quitte le point O. On donne xM = 5,0 m et xN = 6,0 m. Les coordonnées de la balle en fonction du temps sont les suivantes :
x = V0 cos α t
z = - 12 gt2 + Vo sin α t ( je pense que l'équation est fausse est que c'est une erreur de frappe pour l'éditeur, il serait plus logique d'avoir - 1 / 2 gt2 + V0 sin α t )
Donner un encadrement de la valeur de la vitesse Vo qu'il faut communiquer à la balle pour qu'elle arrive sur le green entre les points M et N. Présenter la démarche suivie.
Aide à la résolution 1 : yM = yN = h
Aide à la résolution 2 : t est le même dans les équations donnant x et donnant z
Ce que j'ai trouver :
On veut montrer donner un encadrement de Vo donc :
5 ≤ x ≤ 6 et z=h=1,5m et pour x et y, z est le même
sachant que
x= V0 cos α t ↔ V0 = x/ (cos α t)
et z = - 1 / 2 gt2 + V0 sin α t ↔ V0 = (z+(1/2) g t²)/(sinα t)
alors x/ (cos α t) = (z+(1/2) g t²)/(sinα t) (z+(1/2) g t²)/(sinα t)
Mais à partir de la je suis bloquer je ne vois vraiemnt pas comment répondre à la question. Je vous remercie de bien vouloir m'apporter votre aide s'il vous plait.
Bonjour,
Tu t'y prends mal.
Il te faut isoler " t " à partir de
et reporter cette "expression de " t " dans
Tu obtiendras ainsi l'équation z = f(x) de la trajectoire.
Cette trajectoire passe par le point M (5 ; 1,5) pour la vitesse V01 et par le point N (6 ; 1,5) pour la vitesse V02
V01 et V02 sont les limites de l'encadrement cherché.
Bonjour,
Merci beaucoup de m'avoir répondu.
Du coup j'ai effectuer ce que vous m'avez partager.
Je trouve t= x/ Vo *cos(a) et en le remplacent dans z je trouve z= g*x2/ 2(Vo2 cos (a)2 +sin(a) *x/cos(a)
Dois- je mettre mon expression de gauche sous racine carré ou bien mette a la forme carré celle de droite pour pouvoir les mettre sur le même dénominateur ?
Par la suite l'encadrement de xM et xN, avec V1 etV2 devront-ils être remplacer dans l'équation de z ?
( je suis désolée c 'est une parie que nous avons aborder que très vaguement en cour )
Avant tout il te faut rectifier l'erreur de signe qui figure dans ton expression z(x) de la trajectoire et la simplifier en remplaçant sin( )/cos (
)/cos ( ) par tan (
) par tan ( )
)
On désire que le point M (5 ; 1,5) appartienne à la trajectoire donc que z(5) = 1,5
Cela fournit une équation dont V0 est la seule inconnue.
Résoudre cette équation donne la valeur V01.
Même démarche pour le point N
Du coup en essayant de faire comme vous m'avez dit.J ai ainsi remplacer par tan (a) puis j'ai remplacé toutes les valeurs dont je connaisser mais j'obtient pour z(5)=245/0,24+Vo2 + 13,23
Que dois faire pour trouver un nombre précis ?
Je vous avoue que je suis un peu perdu
Tu dois résoudre l'équation obtenue, mais seulement après avoir rectifié les erreurs de calcul qu'elle contient et bien sûr avoir remplacé z(5) par 1,5m
Si je rectifie je trouve 0, 165 + 1,5Vo 2=- 245 + 13,23
Mai si je réduis le calcul je trouve un nombre négatif et très grand ce qui n'est pas possible ?
D'accord,
pour z (5)= -( g*(5)2/ 2*cos(70)2+ 2Vo2 )+ tan(70) *5
ce qui revient à faire 1,5= - (245/0,11+ 2Vo2) + 13,23
alors (0,11+ 2Vo2)*1,5 = -245 + 13,23
et donc Vo= racine carré de -77,3 environ or on ne peut faire une racine négative
J'ai du mal a voir mon erreur
L'équation de la parabole ( pourtant presque correcte dans ton post du 25-12-18 à 11:34 ) est fausse.
La voici :
Remarque : cos²( ) est un raccourci pour exprimer (cos(
) est un raccourci pour exprimer (cos( ))²
))²
Merci, C 'est donc bien celui que j'ai trouvé or quand je le remplace par z(5) je trouve le résultat que je vous ai fais part un peu plus haut, et qui me semble incohérent
Si j'isole Vo sans remplacer je trouve
Vo=racine carré (2*z(x)*g*x2/ cos2(a)) + racine carré 2*z(x)* x*tan( a)
Diable, Diable dit-il en se grattant la tête ... (V.Hugo)
On va bien arriver à savoir lequel des deux s'est trompé ....
Es tu d'accord aussi avec ce qui suit ?
Oui je suis tout à fais d'accord
Mais si nous essayons le calcul je trouve quelque chose de négatif pas vous ? ( je pense que c'est moi la fautive dans tous ça)
Oui tout à fais et donc nous devrions trouver Vo= 9, 251 ?
Merci je viens de m' apercevoir que c'est lors du passage de Vo que mon calcul est devenu faux
Et si je fais de même pour N je trouve Vo= 10, 03 ?
Et es ce que à partir de la on peut emettre comme hypothèse que Vo est compris entre 9, 251 et 10, 03 ?
Et es ce que à partir de la on peut emettre comme hypothèse que Vo est compris entre 9, 251 et 10, 03 ?
Oui, à ceci près que
a) Les données de l'énoncé comportant seulement 2 chiffres significatifs les résultats que tu donnes sont bien trop précis.
b) Des résultats donnés sans unités sont toujours considérés comme des résultats faux.
Alors j'en conclut que
a) et b) 9, 25 < Vo < 10, 03 m. s
Mais ne pensez vous pas que ces résultats sont trop important pour que la balle puisse arriver jusqu'au green entre les point M et N ?
C 'est - à - dire que si ce résultat est concordant l'exercice est clôt ?
Attention l'unité de vitesse n'est pas le m.s
Bien que l'énoncé reste n'en parle pas ce résultat est obtenu en négligeant la résistance de l'air qui est pourtant importante. En réalité il faudra des vitesses supérieures à celles calculées pour obtenir le résultat cherché.
Mais alors si le calcul 'est pas terminer comment fait-on pour arriver à la fin de celui-ci ?
Par contre l'unité il ne peut y avoir que des m. s ou rien , car je ne vois rien d'autre qui qualifierait la vitesse
Le calcul est terminé.
L'unité de vitesse n'est pas le m.s c'est le mètre par seconde (m/s) ce qui n'est pas du tout la même chose.


