Inscription / Connexion Nouveau Sujet
Solénoïdes coaxiaux
Bonjour, aidez-moi svp
Problème
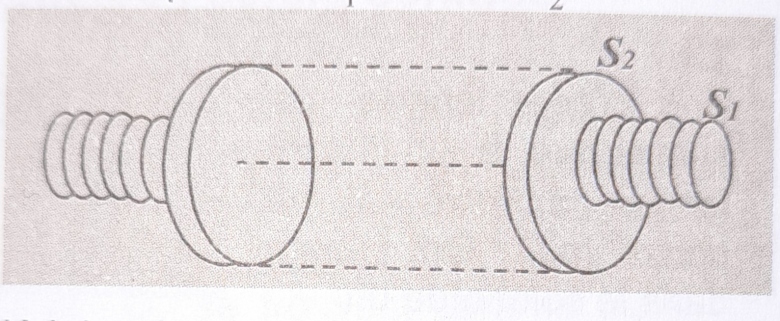
Deux bobines longues S1 et S2 ayant n1 et n2 spires par mètre de longueur sont disposées de manière à avoir le même axe ; cet axe commun est perpendiculaire au méridien magnétique terrestre. Les deux bobines sont placées en série dans un circuit électrique.
On place une petite aiguille aimantée au voisinage de leur centre commun et l'on fait passer dans le circuit électrique un courant d'intensité I.
1) Justifier brièvement pourquoi cette aiguille pivote. Faire un schéma explicatif.
2) Exprimer la déviation 
de l'aiguille par rapport au champ magnétique terrestre en fonction de Bh (composante horizontale du champ magnétique terrestre) et au champ B créé par l'ensemble des deux bobines.
3) Au cours d'une séance de TP deux groupes d'élèves trouvent deux déviations différentes 1 et 2 de l'aiguille telles que tan1 = 3.tan2.
Justifier pourquoi les deux groupes trouvent des angles différents. En déduire la relation entre n1 et n2.
Composante horizontale du champ terrestre : Bh = 2.10-5 T
Bonjour
Toujours la boussole des tangentes avec ici une petite astuce. Qu'as tu fait pour l'instant ? Qu'est ce qui te bloque ?
Ici, très honnêtement je suis bloqué partout.
Je n'ai pas du tout compris le phénomène. Je rencontre beaucoup d'exercices de ce genre où une aiguille aimantée pivote dans une bobine.
Le plus important pour moi, c'est de comprendre le phénomène.
Svp expliquez moi comment faire ce schéma explicatif.
Tape dans un moteur de recherche : "boussole des tangentes" ; tu auras des schémas et des explications.
Ici la boussole est soumise à l'action des trois champs magnétiques ayant pour vecteurs :
* la composante horizontale Bh du champ magnétique terrestre orientée vers le nord magnétique ;
* les deux vecteurs champs créés par les deux bobines ; ces deux vecteurs champ sont colinéaires, de direction commune horizontale et perpendiculaire au vecteur
Établir le courant dans les bobine fait ainsi tourner l'aiguille d'un angle dont la tangente s'exprime simplement en fonction de Bh et de B.
Voici un document sur l'utilisation de la boussole des tangentes. Le champ magnétique étudié sur le document est celui créé par une bobine plate alors que celui de ton exercice est créé par deux solénoïdes coaxiaux mais le principe est le même.
En pratique, il faut bien sûr imaginer les deux solénoïdes à spires non jointives ; sinon : impossible d'observer et de mesurer la déviation de l'aiguille de la boussole !
1) Justification
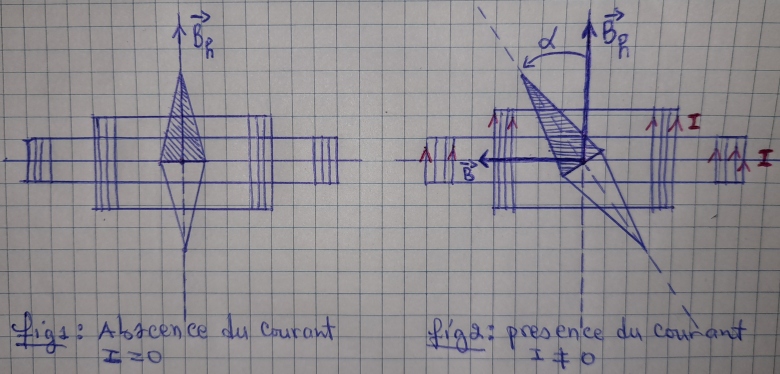
• En l'absence du courant (Figure 1), l'aiguille aimantée est orientée selon la direction et le sens de (composante horizontale du champ magnétique de la terre)
• en présence du courant (Figure 2), l'aiguille est soumise à l'action de deux champs : et
Où (avec
et
les champs magnétiques créés par les bobines 1 et 2.
Conclusion : l'aiguille aimantée prend la direction du champ résultant. Donc elle tournera d'un angle
Oui j'ai compris, grâce à vous ! 
2) Expression de la déviation
Je pose : tan = B/Bh
question 3
Alors je trouve : B = B1 + B2 puisque sont trois vecteurs colinéaires et de même sens.
Donc
Alors
C'est ici où je suis à nouveau bloqué.
Imagine maintenant un élève qui branche les solénoïdes de façon à inverser le sens du courant dans l'un des deux...
Bonjour
Les deux solénoïdes sont associés en série et donc parcourus par des courants de même intensité mais, selon le sens de branchement, le sens des courants peut être le même pour les deux solénoïdes ou les courants peuvent être de sens inverses.
Dans le premier cas, les deux vecteurs champ magnétique ont même direction et même sens : la norme du vecteur somme est la somme des deux normes. Dans le deuxième cas, les deux vecteurs champ magnétiques ont même direction et des sens opposés : la norme du vecteur somme est la différence des deux normes.
Bonjour, je reviens.
Je pose dans ce cas :
Maintenant, si le courant est inversé dans B2, on aura dans ce cas B = B1 - B2
Alors
Donc
Puisque tan1 
tan2, alors 1 de 2.
Annuler
connectez vous