Inscription / Connexion Nouveau Sujet
résoudre avec le repère de frenet
Bonjour.
je n'arrive pas à réussir les question d'un sujet le voici :
pour installer une base de lancement pour fusée , certaines bases sur terre sont plus propice que d'autre , en effet plus la base sera situé près de l'équateur plus la vitesse additionnel due à la rotation de la terre sera grande et donc plus le lancement d'une fusée sera facilité
lorsque la terre fait un tour sur elle même , tous les points de la surface terrestre sont déplacé à la même vitesse angulaire , mais un point situé au niveau de l'équateur a parcouru une distance bien plus importante , sa vitesse linéaire est donc supérieur à celle d'un point situé au niveau du pôle
la latitude est une coordonnée géographique d'un point sur terre re présenté par la valeur angulaire 
au nord ou au sud de l'équateur qui le plan de référence
donnée: rayon de la terre Rt= 6700 km
les questions :
1) déterminer la vitesse additionnel donné par la rotation de la terre à l'équateur par rapport au pôle.
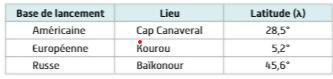
2) déterminer les vitesse additionnel donné au différent lanceurs européen, américain et russe
3) en déduire la meilleur base pour expédier les fusée dans l'espace
le problème c'est que je ne sais pas comment faire pour calculer une vitesse à partir des valeurs d'angle , de plus ils nous avait dit d'utiliser le repère de Frenet mais je vois pas le rapport
je vous remercie énormément pour votre aide
Bonjour
Tu as sans doute vu en cours l'expression du vecteur vitesse dans la base de Frenet ; elle fait intervenir le rayon r de la trajectoire et la vitesse angulaire 
.
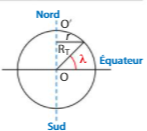
La figure est claire : un peu de trigonométrie permet d'obtenir r en fonction de RT et de .
***Pour le repère de Frenet, lire le §IV : 
Décrire un mouvement***
Bonjour
dans le cours de mon livre j'ai que cette formule de repère de Frenet de plus on pas de mention de vitesse angulaire , en ce qui concerne la valeur de r je trouve qu'on a pas assez de valeur pour la trouver
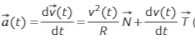
sinon à travers la forme de l'angle je peux deviner qu'il est de 
/4 avec r qui vaut 
2/2 si le rayon du cercle vaut 1 , du coup en utilisant la règle de trois avec le rayon qui vaut 6,7x10^6 m je trouve r= 4,7x 10^6 m (en arrondissant les valeur) , puis en calculant la vitesse avec les deux rayons trouvés je trouve 487 m.s^-1 pour "l'équateur" et 341 m.s^-1 pour "r" , est ce que c'est juste ?
Dans cet exercice, il n'est pas question d'accélération ; il faut simplement calculer la vitesse par rapport au repère géocentrique d'un point à la surface de la terre de latitude l.
Le mouvement étant rectiligne et uniforme, l'expression du vecteur vitesse est :
où est un vecteur unitaire tangent à la trajectoire orienté dans le sens du mouvement. Je t'ai expliqué comment trouver le rayon r de la trajectoire. Je te laisse trouver la vitesse angulaire
...
je suis vraiment désolé
sa fait deux heure que je me creuse la tête , sa serait vraiment plus simple si j'avais la réponse de la première question. étant donné que je suis faible en physique j'essaie tant bien que mal de m'améliorer
sa serait vraiment plus simple si j'avais la réponse de la première
Il faut bien un peu que tu réfléchisses, sinon l'aide ne servirait à rien !
Je t'ai fourni l'expression de la vitesse dans mon message du 02-07-21 à 20:53.
Le rayon r de la trajectoire s'exprime simplement en fonction de RT et de la latitude
. Il suffit de faire un peu de trigonométrie en observant le schéma joint à ton premier message.
La vitesse angulaire s'obtient aussi très simplement sachant que la terre tourne autour de l'axe de ses pôles d'un tour (2
radians) en un jour (durée à exprimer en secondes pour obtenir la vitesse angulaire exprimée en radian par seconde.sin ()=r/Rt et donc r= sin () 
Rt = sin (45) 6700= 4737,6 km ? pour r ?
et = 2/ 3600 24= 7,27 10-5 rad.s-1 ?
donc pour comparer la vitesse entre les deux niveau il faudrait faire :
7.2510-56700103= 485.75 m.s-1 pour le niveau d'équateur
7.2510-54737.6103=
343 m.s-1 pour l'autre niveau
Tu es bien sûr du sinus ? Revois au besoin ton cours de trigonométrie. Sinon, puisque la valeur de est la même pour toutes les bases de lancement, c'est la valeur de "r" qui intervient dans la comparaison.
Réfléchis un peu : à ton avis, pourquoi les européens sont-ils allés installer leur base de lancement en Guyane (à Kourou). Il aurait été plus simple de l'installer en Europe...
D'accord avec ta valeur de .
Annuler
connectez vous