Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. PremièreForum de première PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau première
Partager :

résistances équivalentes

Posté par Apprenti (invité) 23-03-05 à 20:53

Bonsoir , quelqu'un connaitrait il une loi sur les résistances équivalentes car j'ai un circuit et je ne sais pas comment calculer la résistance équivalente , merci .

Posté par Apprenti (invité)re : résistances équivalentes 23-03-05 à 21:18

Sur le shéma suivant , je déduis que toutes les résistances sont en parallèle car elles sont toutes séparées par des neouds , ai je bon?

résistances équivalentes

Posté par
soucoure : résistances équivalentes 23-03-05 à 21:21

Oui moi en gros en parrallèle tu as R_{eq}=\frac{1}{\displaystyle \sum_i{\frac{1}{R_i}}}

et en série tu as R_{eq}=\displaystyle\sum_iR_i

Je ne pense pas qu'on puisse contredire cette relation, mais un ptit schéma est le bien venu, arrives tu à voir la différence en série et parrallèle ?

Posté par
soucoure : résistances équivalentes 23-03-05 à 21:24

Oi merci tu as

R_{eq}=\frac{R_1(R_2+\frac{R_3.R}{R_3+R})}{R_1+R_2+\frac{R_3.R}{R_3+R}}

Voilà je vais qu'en même vérifier...


Non que R et R3 sont en // !

Posté par Apprenti (invité)re : résistances équivalentes 23-03-05 à 21:36

c'est plutot 1/Ri , tu ne crois pas , car dans ta 1ère réponse c'est faux je pense...

Posté par Apprenti (invité)re : résistances équivalentes 23-03-05 à 22:06

alors qui a raison?

Posté par cjipe (invité)re : résistances équivalentes 23-03-05 à 22:06

bonjour

tu as R1 et R3 en parallèles et R2 en serie

Posté par Apprenti (invité)re : résistances équivalentes 23-03-05 à 22:19

je ne comprends plus , c'est pleins de neouds dans le circuit , il ne peut yavoir de résistances en série , bizarre...

Posté par Apprenti (invité)re : résistances équivalentes 23-03-05 à 23:07

?

Posté par Apprenti (invité)re : résistances équivalentes 24-03-05 à 00:01

alors ils sont tous en parallèle car il n'y a que des noeuds entre eux , qu'en dites vous?

Posté par
J-Pre : résistances équivalentes 24-03-05 à 14:11





résistances équivalentes

Posté par Apprenti (invité)re : résistances équivalentes 24-03-05 à 16:08

Je ne comprends franchement rien , est ce qu'ils sont tous en parallèle? et si oui pourquoi ne pas utiliser la formule 1/R , là j'avoue que je ne reconnais pas un seul calcul ni méthode d'analyse

Posté par minotaure (invité)re : résistances équivalentes 24-03-05 à 17:02

salut
malheureusement non ce n'est pas aussi simple.

les resistances ne sont ni toutes en parallele ni toutes en serie.
par contre il faut considerer "localement" le circuit.

voyons les schemas de J-P : il est passe par plusieurs etapes.

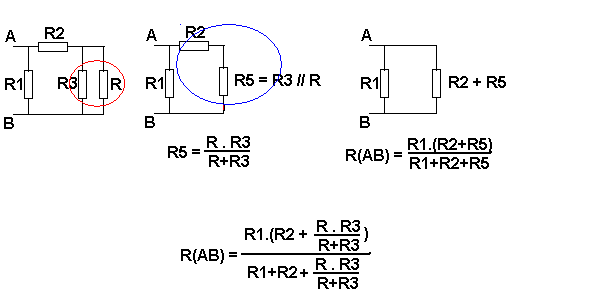
considerons les 2 resistances dans le cercle rouge.
seules, elles sont en paralleles.

soit R5 la resistance equivalente de R3 et de R en parallele.
la formule sur les resistances en parallele nous indique que R5= R*R3/(R+R3)
(remarque ca correspond a 1/R5=1/R+1/R3, il suffit de tout mettre au meme denominateur et de prendre l'inverse et on arrive a R5=R*R3/(R+R3) )
donc on peut effacer nos deux resistances R et R3 et les remplacer par une seule resistance R5.d'où le second schema.


dans le second shema, si on considere seulement R5 et R2, elles sont en serie donc la resistance equivalente de R5 et de R2 est une resistance ayant pour valeur R5+R2
on peut remplacer R5 et R2 par une resistance de valeur R5+R2

dernier chose la resistance  (R5+R2) et la resistance R1 sont en paralleles donc la resistance equivalente des ces 2 la est R(AB)=...
(voir schema)

conclusion la resistance de ce circuit est R(AB).


dans ce genre d'exercice le tout est d'y aller par etape.
a+

Posté par
soucoure : résistances équivalentes 24-03-05 à 18:47

Attention apprenti on a éventuellement G_{eq}=\sum_iA_i mais comme on a aussi R_{eq}=\frac{1}{G_{eq}}\quad\ldots, je te laisse conclure...

Posté par
soucoure : résistances équivalentes 24-03-05 à 18:49

Oups désolé, je suis allé un peu vite c'est G_{eq}=\displaystyle\sum_i\frac{1}{A_i}

Posté par Apprenti (invité)re : résistances équivalentes 24-03-05 à 22:35

ok j'ai compris , et en supposant que je doive écrire la relation : écrire l'équation de la résistance totale Rab en fonction de R , en sachant qur R est réglable , l'écriture 1/R n'est elle pas plus adaptée?
ne donnez surtout pas l'équation , j'attends juste une réponse à ma question svp , merci

Posté par minotaure (invité)re : résistances équivalentes 25-03-05 à 13:07

bah pourquoi ?

du moment que tu as R(AB)=f(R) ou f est une fonction...

par contre pour
"ne donnez surtout pas l'équation , j'attends juste une réponse à ma question svp"

je crois que c'est trop tard, l'un de nous l'a deja donne...
ce n'est pas grave.
tu peux chercher par toi-meme.
tu auras peut etre une autre forme.
apres tu peux regarder si les 2 formes sont egales.(mise au meme denominteur,factorisation...)

Posté par
soucoure : résistances équivalentes 25-03-05 à 13:13

Sinon, ne cherches tu pas à calculer la conductance ?

Posté par Apprenti (invité)re : résistances équivalentes 25-03-05 à 17:07

en fait non personne n'a donné la réponsé héhé , car si je dois établir équation qui permet le calcul de la résistance équivalente de Rab en sachant que R est réglable , je dois donc écrire la relation comme l'a écrit JP , mais je dois mettre un coefficient multiplicateur X devant R , car justement R peut changer de valeur , ce qui me donne :

Rab = R1*((R2+(R3*xR)/(R3+xR)) / R1 + R2 +(R3*xR)/(R3+xR) .

Et x évidemment dépendra de la valeur qu'on veut donner à R...

Posté par
J-Pre : résistances équivalentes 25-03-05 à 17:13

Tu n'as aucune raison d'écrire xR.

Il suffit de prendre la formule que j'ai indiquée (ainsi que d'autres) avec R et de donner à R la valeur voulue dans les calculs.

Si tu veux à toute force employer "x" pour montrer que R est variable, il suffit alors de remplacer R par x dans la formule, mais alors il faut compléter la formule par une phrase telle que par exemple: "Avec x la valeur Ohmique de R". Mais cela n'amène rien de plus.




Posté par Apprenti (invité)re : résistances équivalentes 25-03-05 à 17:22

Ok Jp merci encore de montrer à quel point je me complique la vie pour rien lol .

Posté par Apprenti (invité)re : résistances équivalentes 27-03-05 à 20:52

Si je considère que R1 = 60ohms , R2 = 14 , R3 = 10 et R = 10 , je trouve Rab = 15.04ohm , quelqu'un peut me dire si il trouve la même chose?

J'ai une question du style : pour quelle valeur Rc de R a t'on Rab = Rc = R . Mais je ne sais pas ce que veut dire Rc , quelqu'un a t'il une idée svp?
merci

Posté par Apprenti (invité)re : résistances équivalentes 27-03-05 à 22:39

?

Posté par
dad97re : résistances équivalentes 28-03-05 à 00:42

Bonsoir Apprenti,

Personnellement quand j'ai un circuit comme cela je le "déplie" :

On voit mieux après ce qui est en dérivation et ce qui est en série

Un truc bizarre j'ai la même formule que toi mais je ne trouve pas la même chose , je trouve \rm 14,43 \Omega

Salut

résistances équivalentes

Posté par Apprenti (invité)re : résistances équivalentes 28-03-05 à 01:18

Et sais tu par hasard ce que veut dire Rc , j'ai cherché sur google mais j'ai trouvé aucune doc dessus...

Posté par
dad97re : résistances équivalentes 28-03-05 à 01:33

Re,

Rc est le nom de la valeur de R que tu obtient en résolvant : Rab=R

soit 5$\rm R=\frac{R_1\times (R_2+\frac{R_3\times R}{R_3+R})}{R_1+R_2+\frac{R_3\times R}{R_3+R}}

Salut

Posté par Apprenti (invité)re : résistances équivalentes 28-03-05 à 01:48

Donc Rc par définition c'est quoi , je vois pas franchement , car là il suffit de poser simplement 10  = R1*((R2+(R3*R)/(R3+R)) / R1 + R2 +(R3*R)/(R3+R) , ce qui n'a pas de sens car on a déjà toutes les valeurs des résistances , ça revient ) dire 10 = 15.04 , donc c'est faux , je vois pas du tout où se trouve le Rc , ni à quel est l'intérêt de faire ça...

Posté par
dad97re : résistances équivalentes 28-03-05 à 13:49

Non,

Rc est la solution de l'équation (inconnue R) proposé ci-dessus :

Rc est le nombre (hum pour ton exemple du post de 20:52 il n'y a qu'un Rc qui vaut 15 ohms pour d'autres valeurs j'ai pas fait les calculs en effet on se retrouve avec une équation du second degré)

5$\rm\blue\fbox{%20R_C=\frac{R_1\times%20(R_2+\frac{R_3\times%20R}{R_3+R_C})}{R_1+R_2+\frac{R_3\times%20R}{R_3+R_C}}}

Salut

Posté par Apprenti (invité)re : résistances équivalentes 28-03-05 à 19:53

"Rc est le nom de la valeur de R que tu obtient en résolvant : Rab=R"

franchement je dois être débile car je comprends pas du tout , je vois pas dans l'équation Rab=R où se trouve l'inconnue , on peut écrire Rab = 10 mais dans le Rab ou se trouve l'inconnue , R1 , R20 , R3 , c'est R qui change de valeur peut être?

Posté par
dad97re : résistances équivalentes 28-03-05 à 20:30

Re,

En maths tu n'as jamais vu ce genre de question :

soit f(x)=x+3 Pour quelle valeur Xo de x a t-on f(x)=0

(remplacer f(x) par Rab qui est bien une fonction de R, remplacer Xo par Rc et x par R )

avec R1=60 ohms , R2=14 ohms , R3=10 ohms

3$\rm\blue Rab=R \Longleftrightarrow R=\frac{R_1\times (R_2+\frac{R_3\times R}{R_3+R})}{R_1+R_2+\frac{R_3\times R}{R_3+R}}

3$\blue \rm\Longleftrightarrow R=\frac{60\times (14+\frac{10\times R}{10+R})}{60+14+\frac{10\times R}{10+R}}

3$\blue \rm\Longleftrightarrow R=\frac{60\times (14(10+R)+10R)}{74(10+R)+10R}

3$\blue \rm\Longleftrightarrow R=\frac{8400+1440R}{740+84R}

3$\blue \rm\Longleftrightarrow R(740+84R)=8400+1440R

3$\blue \rm\Longleftrightarrow 84R^2-700R-8400=0

3$\blue \rm\Longleftrightarrow (R-15)(84R+560)=0

et comme 3$\blue\rm R>0 on en déduit donc que 3$\rm\blue R=15 ohms

donc :

3$\rm\blue\fbox{Si R_1=60 \Omega ; R_2=14 \Omega ; R_3=10 \Omega alors la valeur R_C de R tel que Rab=R_C=R est R_C=15 \Omega}



Salut


Posté par Apprenti (invité)factorisation 29-03-05 à 22:02

Bonsoir , si on à cette équation :

84R² - 700R - 8400 = 0

Est ce qu'on peut la factoriser de manière canonique? j'attends simplement un oui ou un non et ensuite je vous montre mon résultat , merci .

*** message déplacé ***

Posté par
Nightmarere : factorisation 29-03-05 à 22:05

Bonjour

La factorisation sous forme canonique est toujours faisable quelque soit le polynôme du second degré .

Par contre , c'est la factorisation entiére qui n'est pas toujours atteignable ( du moin dans \mathbb{R} )


Jord

*** message déplacé ***

Posté par Apprenti (invité)re : factorisation 29-03-05 à 22:17

ok alors ça me donne :

84(R² - 8.3R - 100) = 0
84((R - 4.15R)² - 17,22 - 100) = 0
84((R-4.15R)² - 117.22) = 0
84(R-4.15R-117.22)(R-4.15+117.22)


*** message déplacé ***

Posté par Apprenti (invité)re : factorisation 29-03-05 à 22:17

pas très convaincant je trouve

*** message déplacé ***

Posté par
Nightmarere : factorisation 29-03-05 à 22:18

Il y a un R en trop .. As-tu redévelopper ce que tu as trouvé ?

*** message déplacé ***

Posté par Apprenti (invité)re : factorisation 29-03-05 à 22:33

84(R-4.15-117.22)(R-4.15+117.22)
84(R-15)(R+6.6)


*** message déplacé ***

Posté par Apprenti (invité)re : factorisation 29-03-05 à 22:33

c'est déjà mieux mais je ne trouve pas ça convaincant...

*** message déplacé ***

Posté par
Nightmarere : factorisation 29-03-05 à 22:37

Moi je trouve 28 (R - 15) (3R + 20)


Jord

*** message déplacé ***

Posté par Apprenti (invité)re : factorisation 29-03-05 à 22:48

tu as en fait refactoriser le 84(R+6.6) ? je vois pas trop l'intérêt , par contre ce qui m'étonne énormément c'est qu'un modérateur de ce forum trouve (R-15)(84R+560) , en fait je savais pas qu'on pouvait développer un terme comme ça si ça nous chante lol

*** message déplacé ***

Posté par
Nightmarere : factorisation 29-03-05 à 22:53

Je n'ai pas compris , quel est le probléme ?

*** message déplacé ***

Posté par
infophilere : factorisation 29-03-05 à 22:57

Bonjour

Personnelement je trouve:

\blue \fbox{84(x-15)(x+\frac{20}{3})}=0



*** message déplacé ***

Posté par
dad97re : factorisation 29-03-05 à 22:57

Bonsoir

je ne suis pas modérateur : mais un modeste correcteur

histoire de recadrer le problème :

résistances équivalentes

Salut

*** message déplacé ***

Posté par
Nightmarere : factorisation 29-03-05 à 22:59

Oui , c'est le même résultat que moi kevin

Personnelement j'ai préférer le réduire dans \mathbb{Z} , même si ce n'est pas une réduction compléte , c'est toujours plus agréable aux yeux . mais pour l'équation , ta forme est plus utile


Jord

*** message déplacé ***

Posté par
infophilere : factorisation 29-03-05 à 22:59

PS:J'ai gardé toute les valeurs exactes autrement dit les fractions et je tombe sur un résultat un peut prêt cohérent je pense

Bien évidemment les valeurs de x sont:

\red \fbox{x=15} ou \green \fbox{x=-\frac{20}{3}}

Sauf distraction
Kevin


*** message déplacé ***

Posté par
Nightmarere : résistances équivalentes 29-03-05 à 22:59

Merci Dad97

Posté par
infophilere : 29-03-05 à 23:01

Ah ben oui je n'avais pas remarqué désolé alors d'avoir posté pour rien, enfin nan pas pour rien je m'exerce lol. Bonne soirée à vous deux !

Merci beaucoup pour l'explication des limites et tout le tralala

Bonne nuit (en ce qui me concerne lol)
Kevin




*** message déplacé ***


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !