Inscription / Connexion Nouveau Sujet
Résistance éq
Bonjour!
je suis bloqué
en fait je voulais appliquer le théorème de Kennely(je l'ai vu ur Youtube) pour me débrouiller mais j'arrive pas!!
Bonsoir,
Il faut simplement appliquer les règles que vous avez vues en cours sur les associations de résistances, pas à pas.
Bonsoir YUGI et gts2 ,
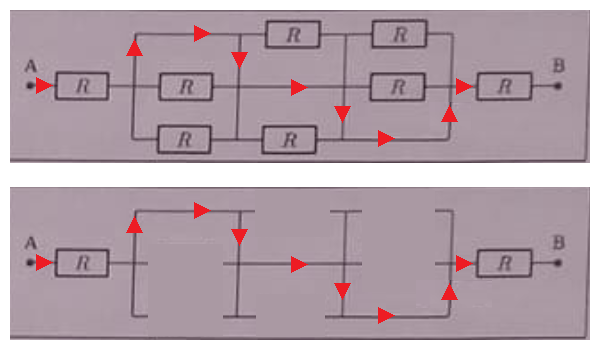
Il me semble qu'on peut simplifier ce réseau en remarquant que beaucoup de ces conducteurs ohmiques sont court-circuités.
Il y a des courts circuits.. on peut pas
@gts2
Oui c'est exactement ce quej'ai remarqué. . Et je trouve que T.Kennely peut servir mais je sais pas comment l'appliquer @odbugt1
Le schéma est très simple.
1- Kennely n'a rien à voir là dedans (vous n'avez que deux bornes).
2- Vous repérez deux résistances disons en //, et vous remplacez par l'équivalent, et dans le cas où l'une est nulle, c'est simple.
3- Et vous recommencez.
Que veut dire : "Il y a des courts circuits. On peut pas". On peut pas faire quoi, appliquer quoi ?
Ce que je voulais dire c'est que je peux pas appliquer la relation de 2 résistance en //..
Car je constate que à l 'entrée du courant (le premier noeud ) il y a 3 branches (2 où l' on trouve une résistance pour chacun et l autre juste un fil conducteur lié à un autre noeud)!
Si on fait uniquement avec deux résistances, on y va pas à pas : entre le premier noeud après A et le suivant : on prend les deux en haut, soit R // 0 qui fait 0 (dit autrement R est court-circuitée) ; il reste R // 0 (ou R court-circuitée) qui de nouveau fait 0.
Le passage à plus de 2 est immédiat :
R1 série R2 série R3 donne (R1+R2) série R3 soit R1+R2+R3
R1 // R2 // R3 donne (1/R1+1/R2) // R3 soit 1/R=1/R1+1/R2+1/R3
Je précise (je ne sais si c'est le problème) : un fil c'est R=0.
On peut aussi utiliser, comme indiqué par @odbugt1, la notion de court-circuit.
Les conducteurs ohmiques court circuités ne sont parcourus par (quasiment) aucun courant.
On peut les débrancher sans que cela perturbe le reste du circuit.