Inscription / Connexion Nouveau Sujet
Régime sinusoïdale
Salut à tous. J'ai un devoir qui me fatigue trop. Pourriez-vous m'aider s'il vous plait?
Voici l'énoncé:
Soient les trois tensions en régime sinusoïdale:
u1=2a cosωt ; u2=a cos(ωt+π/3) et u3=√3/3 a cos(ωt+5π/6)
Démontrer que:
u=4 √3/3 a cos(ωt+π/6).
Mes réponses:
Soit:
U= Umcos(wt+phi)
Cherchons Um
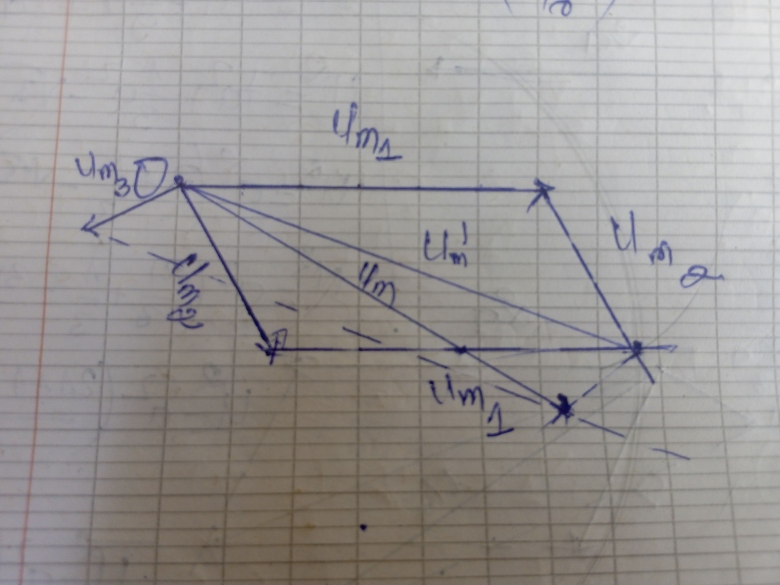
Je crois que je dois faire une construction de Fresnel
Bonjour
A priori on demande une démonstration, pas une simple vérification graphique. Pour cela, tu peux remarquer que 5
/6 - /3 = /2
Cela donne deux vecteurs de Fresnel perpendiculaires.
En plus de ça, je crois que si la représentation graphique est exacte. Peut-être probablement on peut chercher la phase phi et la tension maximale de l'ensemble.
Cordialement
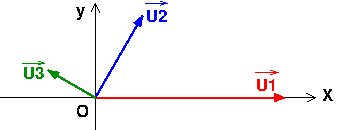
Non ! Si tu représente le vecteur associé à u1 horizontal colinéaire à l'axe (Ox), cela signifie que par convention, l'angle entre (ox) et le vecteur de Fresnel est la phase initiale. Cela n'est pas le cas de ton diagramme.
Puisque les vecteurs de Fresnel vérifient :
Tu peux projeter sur les deux axes comme tu est habitué à le faire pour les vecteurs forces :
ayant ces deux composantes, tu sais que la norme du vecteur somme est l'amplitude de la tension et tu sais que la phase initiale est l'angle entre l'axe (Ox) et le vecteur .
Annuler
connectez vous