Bonjour quand même...

Et où est-il ton problème ?


*** message déplacé ***

merci a ceux qui s'attarderont sur mon problème.

BONJOUR. j'aimerais résoudre un probleme de phisique:
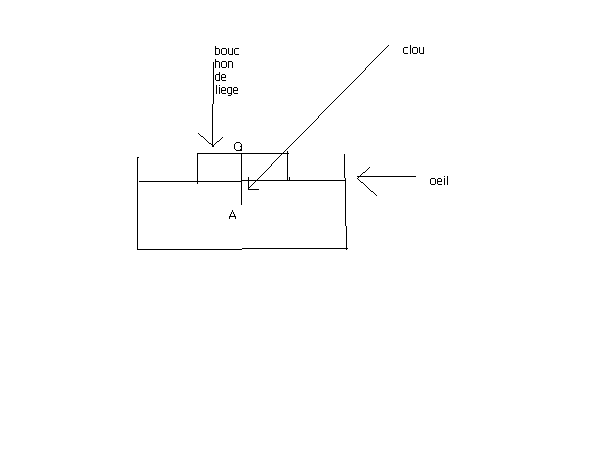
Un bouchon de liege de rayon 6cm est transpercé en son centre par un clou OA.
Le tout flotte a la surface de l'eau. On regarde de facon rasante la surface de l'eau(voir schéma).

*****************************************************************************

Déterminez a partir de quelle hauteur OA, on ne voit plus le clou.


Je ne vois pas du tout comment résoudre ce problème avec les infortmations que l'on a.

MERCI beaucoup

excuse moi jme suis trompé regarde mon otre topic si tu veux bien m'aidé merci a toi

*** message déplacé ***

Bonjour,

Bienvenue sur l' pour ton premier problème !

On a besoin de deux informations supplémentaires :
. quelle est l'épaisseur du bouchon (à moins de considérer que le point O est à la surface de l'eau)
. quel est l'indice de réfraction de l'eau ?

J'y suis.


*** message déplacé ***

bonjour a toi et merci!!
eh bien l'indice de réfraction de l'eau et de 1.33 et pour l'épaisseur du bouchon je ne sais pas!!dsl

MERCI!!!!

*** message déplacé ***

Tu sais qu'il y a un angle limite de réfraction quand on passe d'un milieu à un autre qui a un indice de réfraction plus faible. C'est le cas ici puique le rayon lumineux issu du point A, l'extrêmité du clou, passe de l'eau d'indice de réfraction 1,33 à l'air d'indice de réfraction 1

Applique la loi de Snell-Descartes

la loi:
i1 sin1= i2 sin2 ???????

n₁ vaut 1,33
i₁ est un angle que l'on cherche
n₂ vaut 1
i₂ ne peut pas être plus grand que 90°, auquel cas sin(90°) = 1

Merci a toi pour t'étre pencher sur mon probleme. merci beaucoup!!!! et bonne fete de fin d'année!!!!

Je t'en prie. Bonnes fêtes à toi aussi !
A une prochaine fois !

excuse moi de te redéranger mais j'ai encore un petit problème a régler: j'ai trouvé l'angle i1 qui vaut 49degré mais je ne vois toujours pas comment trouver la taille du clou et mon pere non plus^^!! merci

Considère le triangle rectangle sous le bouchon :
petit côté : le clou dont on cherche la taille
grand côté : le rayon du bouchon de liège : 6 cm
Considère aussi les angles alternes-internes de valeur 49° (c'est bon !)

Si on considère que la face inférieure du bouchon est au niveau de la surface de l'eau et que l'on calcule la longueur du clou qui dépasse sous le bouchon, alors,

clou * tg(49°) = 6 cm
(avec les notations modernes qui sont celles des calculettes qui viennent des USA) clou * tan(49°) = 6 cm

D'où

clou = 6 / tg(49°) 5,26 cm 53 mm

Bonjour à ton père !

OK merci beaucoup pour ton aide je crois que c'est bon cette fois-ci ok je lui passerais le message!!! encore merci et a bientot!!!

Je t'en prie.
A bientôt !

réfraction de la lumiere

*** message déplacé ***