Inscription / Connexion Nouveau Sujet
radioactivité de l'iode 131
bonjour, j'aurais besoin d'un petit coup de main pour cet exo, merci.
1) l'iode 131 est radioactif (Beta -). écrire sa désintégration radioactive en sachant que son n° atomique est 53.
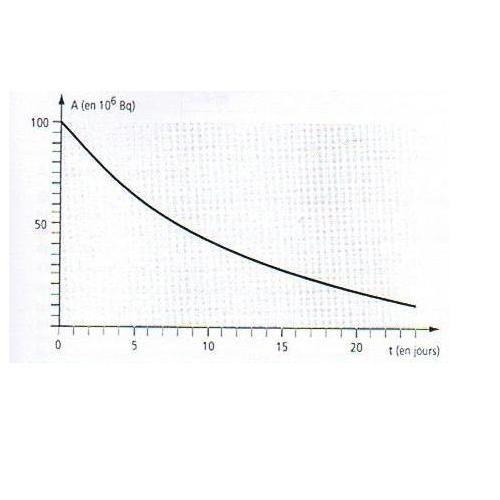
2)la courbe ci-dessous représente, en fonction du temps exprimé en jours,l'activité,exprimée en million de becquerel,d'un echantillon d'iode contenant de l'iode 131:
deduire de cette courbe la durée nécessaire pour que l'activité soit divisée par 2 et la durée nécessaire pour qu'elle soit divisée par 4. en deduire la demi-vie de l'iode 131.
3)determiner en j^-1 et en s^-1 la constante radioactive lambda de l'iode 131.
4)indiquer sans demonstration,l'expression de la loi de variation de l'activité d'un echantillon d'iode contenant de l'iode 131 en notant A0 son activité initiale et en deduire,en jours,la durée nécessaire pour que l'activité soit egale à 80% de l'activité initiale.
verifier ce resultat sur la courbe.
5)calculer le nombre initial de noyaux d'iode 131 dans l'echantillon d'iode dont l'activité initiale vaut 1,0.10^8 Bq.
mes reponses:
1) c'est ok.
2)t=8 jours(durée nécessaire pour que l'activité soit divisée par 2)=> demi-vie de l'iode 131 T=8
t=16 jours (durée nécessaire pour que l'activité soit divisée par 4)
3)constante radioactive de l'iode 131 =environ 8,7.10^-2 J^-1
constante radioactive de l'iode 131 = environ 1,003.10^-6 s^-1
4) et 5) je n'arrive pas.
2)
Tu écris: demi-vie de l'iode 131 T=8
8 quoi ? une grandeur physique sans unité ne veut rien dire.
-----
3)
OK
-----
4)
A(t) = Ao.e^(-8,7.10^-2.t) avec t en jours.
Activité egale à 80% de l'activité initiale pour t = t1 tel que :
0,8.Ao = Ao.e^(-8,7.10^-2.t1)
0,8 = e^(-8,7.10^-2.t1)
ln(0,8) = -8,7.10^-2.t1
t1 = ln(0,8)/(-8,7.10^-2) = 2,6 jours
-----
5)
N(t) = No.e^(-8,7.10^-2.t)
A(t) = -dN/dt = 8,7.10^-2.No.e^(-8,7.10^-2.t)
A(0) = 8,7.10^-2.No = 1,0.10^8
No = 1,1.10^9
-----
Sauf distraction. Vérifie. 
on peut faire aussi avec No=Ao/ avec Ao=1.0*108
avec Ao=1.0*108
No=1.0*108/8.7*10-2
No=(1/8,7) *1010
No=1.15 *109 ??
Ce n'est pas différent de ce que j'ai écrit dans ma réponse du 29-01-10 à 14:05
Mais, les données étant à 2 chiffres significatifs, la réponse doit aussi l'être.
No = 1,1.10^9

Bonjour, bonjour,
j'ai le même exercice et j'ai tout résolu sauf un truc que je ne comprends pas.
Comment avez-vous fait pour passer de 0,8 = à ln(0,8) =
? pourquoi logarithme néparien de 0,8 ?
non je ne comprends pas. je vois bien qu'il faut utiliser la formule de type :
T = mais je ne vois pas pourquoi logarithme néparien de 0,8.
Dans la formule T = ln(2)/Lambda, T est la période de demi vie de l'élément radioactif.
Ici ce n'est pas ce qu'on te demande.
A partir de 0,8 = e^(-8,7.10^-2.t1)
On prend le logarithme népérien des 2 membres --->
ln(0,8) = ln[e^(-8,7.10^-2.t1)] et si on se rappelle ce que signifie "logarithme népérien", on a immédiatement :
ln(0,8) = -8,7.10^-2.t1
...

bonsoir a tous
j ai le meme exercice
et enfaite pour le 2)
on peut dire directement cela ?
t=8 jours(durée nécessaire pour que l'activité soit divisée par 2)= demi-vie de l'iode 131 T=8
t=16 jours (durée nécessaire pour que l'activité soit divisée par 4
que la demi vie est 8s car c est la moitie ?
merci d avance
ATTENTION aux unités.
L'abscisse de l'abaque est graduée en "JOURS"
Et donc tu t'es trompé en écrivant :
"que la demi vie est 8s car c est la moitie ?
C'est 8 jours et pas 8s

bonjour 
a oui merci
mais est ce qu on peut metre que cela ?
t=8 jours(durée nécessaire pour que l'activité soit divisée par 2)= demi-vie de l'iode 131 T=8 jours
t=16 jours (durée nécessaire pour que l'activité soit divisée par 4
donc la demi vie est 8jous car c est la moitie
et je donne la deffinition de demi vie
cela suffie ?
merci encore




