Inscription / Connexion Nouveau Sujet
Radioactivité
Bonjour j'ai besoin de votre aide svp
Exercice :
Le nucléide du cadmium 10748Cd est radioactif 
+ . Sa période est T=6h 42min .
1. Definie la période d'un élément radioactif .
2. Écris l'équation bilan de la désintégration de ce nucléide.
3. Un échantillon de 10748Cd a une masse mo à la date t=0.
Détermine la fraction de mo qui sera désintégré au bout de 20h 6min.
Données :
Célérité de la lumière dans le vide: 3.108 m/s, 1 MeV=1,6.10-13 J
Extrait du tableau périodique des éléments : 45Rh ; 46Pd ; 47Ag ; 48Cd ; 49In ; 50Sn ; 51Sb
Réponses:
1. La période d'un élément radioactif est le temps nécessaire pour que la moitié des noyaux initiaux de cet élément soit désintégrée.
2.
De façon générale , on a :
10748Cd 
AZX + 01e
* Appliquons les loi de conservation du nombre de masse et du nombre de charge.
_ Conservation du nombre de masse : 107=A+0 
A=107 nucléons
_ Conservation du nombre de charge : 48=Z+1 Z=47 protons
D'où , d'après l'extrait du tableau périodique des éléments , l'équation de désintégration devient :
10748Cd 10747Ag + 01e
3.
Bonjour,
Tes réponses aux questions 1 et 2 sont bonnes.
Pour la question 3 il faut penser à comparer les valeurs de la période à celle de la durée de la désintégration.
Bonjour,
Tes réponses aux questions 1 et 2 sont bonnes.
Pour la question 3 il faut penser à comparer les valeurs de la période à celle de la durée de la désintégration.
D'accord
La période T=6h 42 min =6,7h
La durée de la désintégration t1=20h 6min =20,1 h
On remarque que t1=3T
Oui, c'est exact.
Il s'agit donc de trouver la fraction de m0 qui se sera désintégrée au bout d'une durée égale à trois périodes.
Désolé
C'est la question que je ne comprends pas!
La fraction de mo , comment ça ?
Soit N0 le nombre de noyaux radioactifs non désintégrés à la date t=0 et soit m0 la masse de ces noyaux.
Que peut on dire du nombre N et de la masse m des noyaux non désintégrés restants
a) A la date t = T ?
b) A la date t=2T ?
c) A la date t= 3T ?
Soit N0 le nombre de noyaux radioactifs non désintégrés à la date t=0 et soit m0 la masse de ces noyaux.
Que peut on dire du nombre N et de la masse m des noyaux non désintégrés restants
a) A la date t = T ?
b) A la date t=2T ?
c) A la date t= 3T ?
* À la date t=T
N=N0.e-
T
N=N0/2
m=n×M
=(N/N0)×A
m=A/2
* À la date t=3T
N=N0e-3
T
N=N0/8
m=n×A
=(N/N0)×A
m=A/8
Tu y es presque.
Ton résultat peut être obtenu autrement :
A la date t=T, compte tenu de la définition de la période il reste N(T) =N0 / 2 noyaux non désintégrés.
A la date t = 2T le nombre de noyaux restants est à nouveau divisé par 2, puis encore par 2 à la date t=3T
On a donc N(3T) = N0 / 2³ = N0 / 8
La masse m(t) des noyaux étant proportionnelle à N(t) on a aussi m(3T) = m0 / 8
Ce qui veut dire aussi qu'à la date t=3T il ne reste que 1/8 de la masse initiale
Cependant, en relisant la question posée on constate que la question ne porte pas sur la proportion de la masse restante (non désintégrée) mais sur celle de la masse ayant été désintégrée.
Je te laisse terminer.
Lis l'énoncé :
On ne te demande pas de trouver une masse, mais la fraction de masse initiale qui a été désintégrée.
On l'obtient à partir de la fraction de masse initiale qui n'a pas été désintégrée.
mo/8 est la fraction de masse qui n'a pas été désintégrée , la fraction de masse qui a été désintégrée est : m0-m0/8=(7/8).m0
C'est exact.
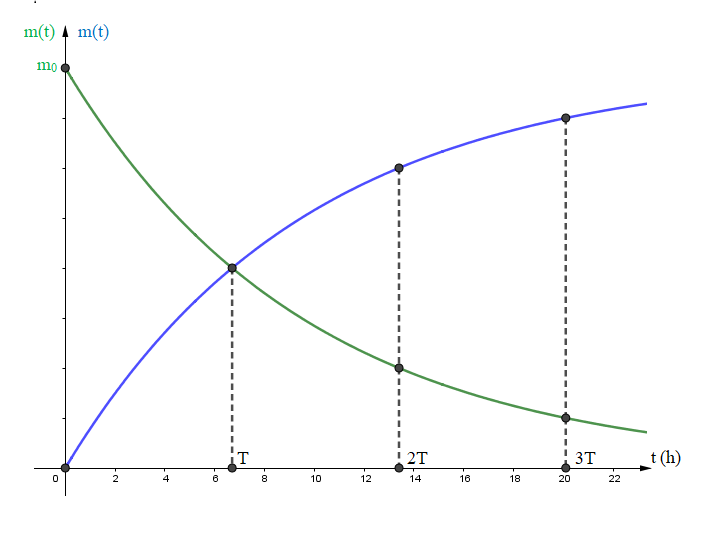
Ci dessous les graphiques donnant l'évolution en fonction du temps de la masse désintégrée ( en bleu ) et celle de la masse restante non désintégrée (en vert).
Annuler
connectez vous