Inscription / Connexion Nouveau Sujet
Quantité de mouvement
Bonjour, je veux un peu d'aide pour cette question.
ÉNONCÉ
On comprime à l'aide d'un ressort de raideur k et de longueur à vide = 25cm, d'une longueur
= 5cm et on le libère sans vitesse initiale. Le solide (S) percute une bille (B) de masse m placée en B. Le choc est parfaitement élastique. Les frottements sont supposés négligeables sur toutes les parties sauf sur (BC).
On donne, M= 30g : m=10g ; g=10m/s² ; k=300 N/m
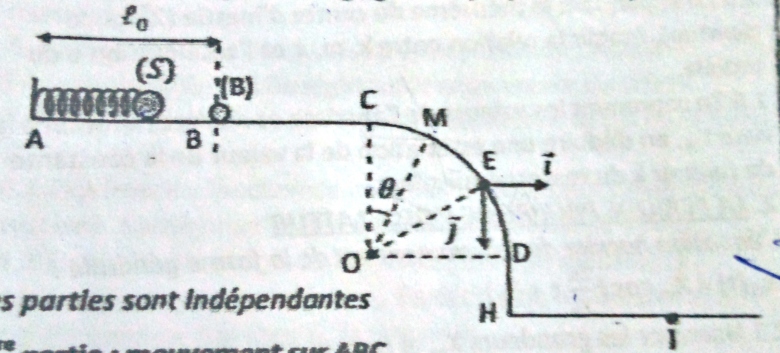
1.Déterminer la vitesse du solide (S) au point B juste après le choc.
2. Montrer que la vitesse de la bille (B) après le choc vaut
= 7,5m/s
Mes réponses
1.
Inventaire des forces extérieures :
en appliquant jusqu'au bout j'obtiens = 5m/s
2. Je n'arrive pas à faire.
Mais je sais que c'est par la quantité de mouvement qu'il faut procéder
Bonjour,
Utilise la conservation de la quantité de mouvement ainsi que celle de l'énergie cinétique.
Bonjour, j'aimerais bien de l'aide pour cette question.
ÉNONCÉ
On comprime à l'aide d'un ressort de raideur k et de longueur à vide = 25cm, d'une longueur
= 5cm et on libère sans vitesse initiale. Le solide (S) percute une bille (B) de masse m placée en B. Le choc est parfaitement élastique. Les frottements sont supposés négligeables sur toutes les parties sauf sur (BC).
On donne M = 30g ; m = 10g ; g = 10m/s² ; k = 300 N/m
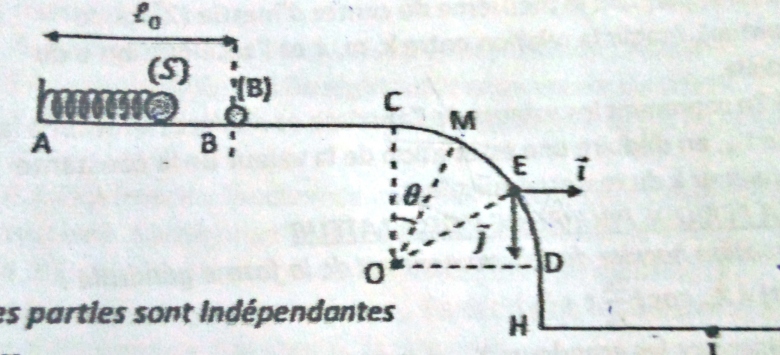
1. Détermine la vitesse du solide (S) au point B juste après le choc
2. Montrer que la vitesse de la bille (B) après le choc vaut
= 7,5m/s.
Ce que j'ai fait
1-
En appliquant la conservation de l'ernergie mécanique on a :
j'obtiens = 5m/s
pour la 2e question je suis bloqué je ne maîtrise pas bien les quantités de mouvements.
*** message déplacé ***
Bonjour,
Tu as déjà posté cet exercice le 26-06-20 à 08:34 sous le titre de " Quantité de mouvement " et tu n'as pas répondu au début d'aide qui t'a été apportée.
Le règlement de ce forum interdit de poster plusieurs fois le même sujet.
*** message déplacé ***
Bonjour,
@pfff : le multi-post est strictement interdit sur le forum  . Tu es loin d'être nouveau sur les
. Tu es loin d'être nouveau sur les  , tu dois donc respecter la règle :
, tu dois donc respecter la règle :
Je propose à pfff de reprendre cet exercice en apportant une proposition de réponse ( ou bien des questions précises) à mon post du 26-06-20 à 09:52
Bien entendu, la définition de la quantité de mouvement est supposée connue, sans quoi il n'est pas possible de répondre.
 Je suis désolé je savais plus si j'avais déjà posté cet exercice. Et j'ai pas pris la peine de vérifier dans Mes messages. Encore mille excuses
Je suis désolé je savais plus si j'avais déjà posté cet exercice. Et j'ai pas pris la peine de vérifier dans Mes messages. Encore mille excuses 
L'énoncé indique que le choc est parfaitement élastique.
Il en résulte que (S) et (B) ne restent pas solidaires après le choc et que chacun des deux repart avec une vitesse qui lui est propre.
Soit la vitesse de (S) juste après le choc :
La conservation de la quantité de mouvement s'écrit :
Soit après projection sur l'axe AC :
Cette équation possède deux inconnues, il faut donc une deuxième équation pour répondre à la question posée.
Cette deuxième équation est fournie par la conservation de l'énergie cinétique (choc parfaitement élastique.
la conservation de l'énergie cinétique
vous vouliez dire le théorème de l'énergie cinétique ?
si oui je l'applique de ou à ou car je ne vois pas encore
vous vouliez dire le théorème de l'énergie cinétique ?
Non
Conservation de l'énergie cinétique du système {S + B} :
Energie cinétique du système {S + B} avant le choc = Energie cinétique du système {S + B} après le choc
Conservation de l'énergie cinétique du système {S + B} revient à :
Energie cinétique de S avant le choc + Energie cinétique de B avant le choc =
Energie cinétique de S après le choc + Energie cinétique de B après le choc
C'est bon.
Bien entendu tu auras tout intérêt à simplifier :
Il ne reste plus qu'à résoudre le système d'équations dont tu disposes pour trouver l'expression
puis la valeur de v2
Divise l'équation (2) par l'équation (1) et simplifie le résultat obtenu. Tu obtiens une équation (3)
En combinant les équations (1) et (3) tu obtiens une équation (4) qui permet de calculer v2
Remarque :
Mathématiquement, la division de (2) par (1) n'est possible que si v1 v'
v'
Mais physiquement on peut écarter le cas où v1 = v'
Pourquoi ?
Indices :
a) Utiliser une ou l'autre des équations établies le 17-07-20 à 23:08 pour calculer v2 dans l'hypothèse ou v1 = v'
b) Se souvenir que v1 est la vitesse de (S) avant le choc, v' la vitesse de (S) après le choc, v2 la vitesse de (B) après le choc.
En effet.
Nous sommes dans le cas ou le choc n'a pas eu lieu.
Les vitesses de (S) (5m/s) et de (B) (0m/s) restent les mêmes.
Or l'énoncé précise qu'il y a eu choc.
On peut donc écarter le cas ou v1 = v' (et v2=0)


 ) :
) :




