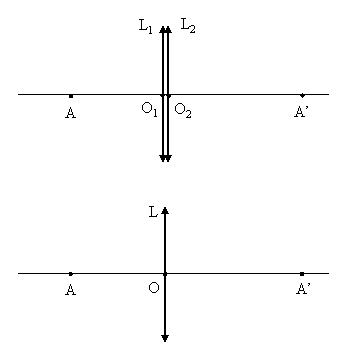La vergence C, c'est tout simplement une valeur pour déterminer le pouvoir divergent ou convergent d'une lentille : elle sert dans la vie courante principalement aux opticiens qui choisissent les lunettes adaptés à la vue de chacun et donc avec un vergence spécifique. Ce n'est qu'une notion de plus à acquérir ! Ce qu'il faut que tu te souviennes, c'est que c'est l'INVERSE (et non pas le contraire) de la distance focale ! Et ainsi dans un exercice, si tu as besoin de la distance focale pour le résoudre, regarde si on ne te donne pas la vergence ou inversement !

Donc ce que tu dois retenir :

La vergence C mesurée en (dioptries) est l'inverse de la distance focale f' et sert d'outil de travail aux opticiens et oculistes.
On peut écrire : C () = f ' ^-1 = 1/f ' avec f ' en m

bonjour,

La vergence d'une lentille (exprimée en dioptrie) correspond à l'inverse de la distance focale f' de la lentille (exprimée en m).

l'utilité de la vergence est surtout en ophtalmologie (les verres de lunettes qui sont des lentilles sont exprimées en dioptries sur les ordonnances).

Cela permet d'avoir une unité plus parlante que les distances focales....

c'est clair?

on a posté en même temps.

hi hi hi

Pire que d'avoir posté en même temps, on a écrit à peu de chose près la même chose !

hé hé hé !

Merci à vous deux pour vos réponses !

Le truc que je ne comprend pas bien c'est que finalement j'ai l'impression que la vergence ça a la même utilité que la distance focale non ? (hormis le fait que ça soit exprimé en dioptries)

Et une autre question, le foyer objet je peux dire que c'est le contraire du foyer image ?

Merci =)

Quelqu'un pour répondre à mes autres interrogations siouplaît ?

Bonjour Syska,

c'est vrai ca, ils sont tellement contents d'avoir posté la meme chose au meme moment que du coup ils t'ont oublié !
Alors voici la réponse à tes deux interrogations :

a) utilité de la vergence : d'abord la relation de conjugaison des lentilles (-1/OA + 1/OA' = 1/OF', OA, OA' et OF' étant des mesures algébriques) te montre qu'en optique on travaille plus souvent avec les inverses qu'avec les grandeurs réelles. Il est donc naturel de donner un nom à l'inverse de la distance focale, cad la vergence C, et de se servir de C. bien souvent les applications numériques ent sont facilitées.
Ensuite, on te montrera peut-etre en cours que lorsqu'on accole (cad quand on les plaque l'une sur l'autre) deux lentilles minces de vergences C₁ et C₂, alors la vergence de l'ensemble est C = C₁ + C₂, et cela quelle que soit la nature (convergente ou divergente) des deux lentilles : c'est pas plus simple comme ça ? (si ca t'intéresse je t'enverrai la démonstration sur simple demande, mais pas maintenant).

b)  "le foyer objet je peux dire que c'est le contraire du foyer image" :
ca dépend de ce que veut dire "contraire" pour toi : oOvinceOo a déjà signalé que tu confondais avec inverse...
Le foyer objet f d'un système optique est un objet dont l'image donnée par ce système se trouve à l'infini ; le foyer image F' est l'image d'un objet placé à l'infini. F et F' ont donc des propriétés similaires, l'un en tant qu'objet et l'autre en tant qu'image. Mais on ne peut pas dire que l'un est le contraire de l'autre.

A bientot,  Prbebo.

Merci prbebo pour tes réponses !

a) Tout exemple ou aide est bonne à prendre donc oui je veux bien la demonstration s'il te plait

b) Je pensais que c'était son contraire du fait que OF'= -OF et que F' est toujours le symétrique de F.

Bonjour Syska,

voici d'abord la reponse a ta question b : j'ai bien compris ce que tu voulais dire en parlant e contraire, mais ce n'est pas le mot que tu aurais du employer. En mathematiques, aud deux grandeurs a et b sont telles que b = -a, on dit que b est l'oppose de A. Pas l'inverse ni le contraire ! Et ne crois pas que je chicane pour rien : dans une copie d'examen (le bac par exemple), un correcteur ne sera peut-etre pas aussi indulgent. Alors mieux vaut s'y faire le plus tot possible...

Question b, formule dse vergences. Voici la demonstration, avec la figure ci-jointe :

Soient deux lentilles L1 et L2, accolees cad que leurs centres optiques O1 et O2 sont quasiment confondus (a l'epaisseur du verre pres). Sur mon schema, par j'ai dessine deux lentiles convergentes, mais tu verras que la demonstration ci-dessous est generale et s'applique aux trois autres situations (L1 conv. et L2 div., L1 div. et L2 conv., L1 et L2 div.). On appelle la distance focale de L1 et celle de L2. Pour ne pas encombrer le schema, je n'ai pas dessine la position des quatre foyers F1, F'1, F2 et F'2.

Soit un objet lumineux A, ponctuel et place sur l'axe optique commun aux deux lentilles. On cherche l'image A' de A obtenue apres que les rayons aient traverse les deux lentilles. On a affaire a un systeme optique a deux composants (L1 et L2) donc on applique la demarche de calcul suivante :
A  -----(par L1)----->  A1  -----(par L2)----->  A'
La premiere fleche indique que pour L1, A est un objet dont on appelle A1 l'image (c'est l'image qu'on observerait s'il n'y avait pas L2) ; la deuxieme fleche indique que le point A1, image pour L1, devient pour L2 un objet dont L2 fournit une image A'. A' est alors l'image de A donnee par le systeme (L1, L2).
Comprends-tu cette demarche ? Si on avait une troisieme lentille L3, on ecrirait A  -----(par L1)----->  A1  -----(par L2)----->  A2  ----->(par L3)----->  A' : la sortie du premier systeme devient l'entree du suivant,  et ainsi de suite.

a) passage de A a A1 : j'ecris la relation de conjugaison avec A pour objet, A1 pour image et avec la distance focale de L1, soit -1/ + 1/ = 1/ = C1, relation 1. La quantite C1 = 1/1/ est la vergence de L1.
b) passage de A1 a A' : j'ecris de meme la relation de conjugaison avec maintenant A1 pour objet, A' pour image et avec la distance focale de la lentille L2, soit -1/ + 1/ = 1/ = C2 ; mais, comme O2 est quasiment confondu avec O1, je peux recopier cette relation en remplacant O2 par O1, ce qui donne -1/ + 1/ = C2, relation 2.

Pour obtenir une relation faisant passer directement de A a A', sans passer par l'image intermediaire A1, il suffit dans ce cas tres simple d'additionner les relations 1 et 2, ce qui donne : -1/ + 1/ = C1 + C2. Cette derniere relation est identique a l'equation de conjugaison d'une lentille mince unique, L, placee en O (O = O1 ou O2, c'est pareil), et de vergence C = C1 + C2 (donc de distance focale equivalente telle que 1/ = 1/ + 1/.

Voila, j'ai bien demontre que deux lentilles accolees de vergences C1 et C2 sont equivalentes a une lentille unique de vergence C = C1 + C2 et placee bien sur au meme endroit. Voir le 2ieme schema ci-dessous. Et comme cette demonstration n'a fait aucune hypothese sur la nature (convergente ou divergente) des lentilles, ce resultat est general.

Maintenant, tu vas sans doute me dire "et si les lentilles n'etaient pas accolees mais separees par une distance O1O2 non nulle ?" (de toutes facons si tu ne me le dis pas, je devance la  question...). Dans ce cas ma demo ne marche plus mais la demarche (A -> A1 -> A') peut toujours etre appliquee. On arrive alors a une expression de la vergence equivalente donnee par une relation appelee "formule de Gullstrand". Mais pas question de te la demontrer, car c'est tres largement au-dessus du programme d'optique de premiere ! Si ca t'interesse tu peuxc consulter le site suivant :
http://fr.wikipedia.org/wiki/Formule_de_Gullstrand
Dans ce site les vergences sont notees V au lieu de C, et la distance algebrique e = H'1H2 est simplement O1O2, pour des lentilles minces. Si tu es curieux, tu verras tout de suite que lorsque e = 0 (lentilles acolees) on retrouve bien C1 + C2.

A bientot pour d'autres topics.  Prbebo.