Inscription / Connexion Nouveau Sujet
Problème Mécanique
Salut à tous,
je bloque sur un petit problème, le voici:
(cf image)
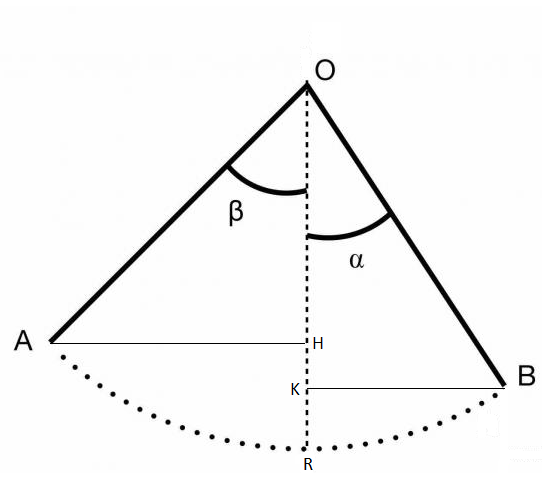
Un acrobate part du point A avec une vitesse nulle sur un trapèze décrivant un arc de cercle de rayon R = 10 m autour du point O.
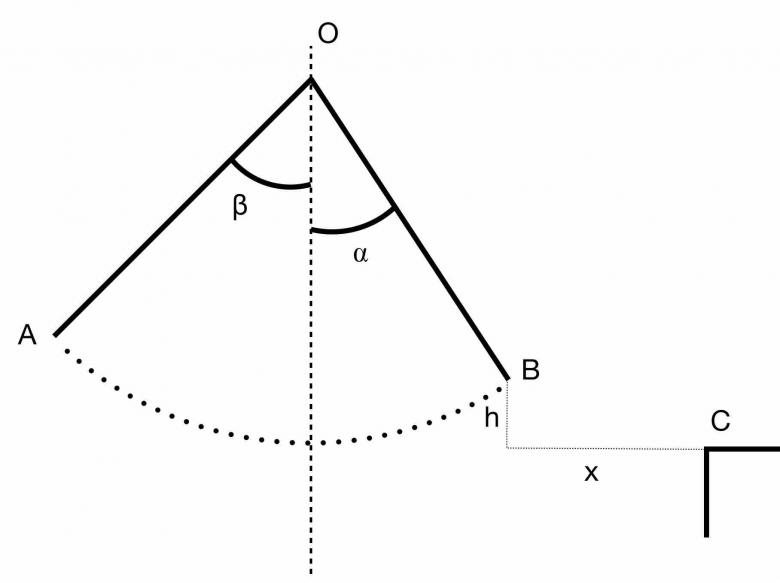
Il lâche le trapèze au point B avec une vitesse de 6 m/s pour retomber au point C sur une plateforme située h = 1,5 m plus bas que B
Sachant que Alpha = 40 deg
Calculez Beta
Calculez X ( la distance horizontale entre B et C)
Voila je ne sais vraiment pas quoi faire. J'ai essayé de partir avec la vitesse angulaire mais ça ne m'a rien donné.
Merci de votre aide 
Bonjour,
Bien que l'énoncé ne le précise pas, on suppose que les forces de frottement sont négligées.
Question 1:
Choisir un niveau de référence pour les énergies potentielles de pesanteur et appliquer la conservation de l'énergie mécanique entre A et C
Question 2 :
C'est un problème classique de chute parabolique.
Attention !
J'ai fait une faute de frappe.
Il faut lire :
Question 1:
Choisir un niveau de référence pour les énergies potentielles de pesanteur et appliquer la conservation de l'énergie mécanique entre A et B ( et non entre A et C )
Bon c'est vrai la question 2 était facile:
Axe Vertical c'est un mouvement rectiligne uniformément accélérée du coup en calcul le temps et on injecte le temps dans le mouvement rectiligne uniforme sur l'axe horizontale.
Merci
Mais pour la question 1, je ne vois pas le lien entre les énergies et l'angle, on pourrait écrire :
Avec K la hauteur au milieu du parcours sur l'arc de cercle
mais je bloque toujours
merci
Soit R le niveau de référence des énergies potentielles de pesanteur :
En A :
EcA=0
EpA = m*g*HR = m*g (OR-OH) = m*g (R - R* cos β) = m*g*R (1 - cos β)
EmA = EcA + EpA = m*g*R (1 - cos β)
En B :
EcB= ½ * m * (VB)²
EpB = m*g*R (1 - cos α)
EmB = ½ * m * (VB)² + m*g*R (1 - cos α)
EmA = EmB
Je te laisse terminer