Inscription / Connexion Nouveau Sujet
Problème lentille
Bonjour j'arrive pas à comprendre cette exercice:
6.
A) A qu'elle distance d'une lentille de 16 cm de focale faut il placer un objet pour en obtenir une image réelle 4 fois plus grande que l'objet
B) Meme question que ci-dessu, mais pour obtenir une image virtuelle
Merci pour votre aide 
Bonjour Soph2341,
En optique, il est toujours utile de faire un schéma ☺️.
Es-tu à l'aise avec les notions de distance focale, image réelle, image virtuelle ?
Indice: sachant que la distance focale est positive. A ton avis, la lentille est convergente ou divergente ? ☺️
Bon courage,
Metal Oxalate
Bonjour merci pour votre réponse :
Alors oui la distance focale c'est la distance entre le foyer et la lentille
Image réelle cela veut dire qu'on peut placer un écran et on vera l'image sur l'écran alors que si c'est virtuelle non
Si la distance focale est positive alors celle ci est convergente
J'ai des souci au moment d'appliquer la formule:
1/f = 1/p + 1/p'
je ne sais pas du tout comment faire pour résoudre algébriquement ? 
Si je représente tous cela comme on m'a conseillé je sais que je dois mettre mon image après le foyer pour avoir une image réelle
Et si on applique la formule de l'agrandissement qui est G= - P/P' = - 4 (l'agrandissement) et du coup on obtient p' = 4 x P
Mais après je suis bloqué je ne sais plus quoi faire 
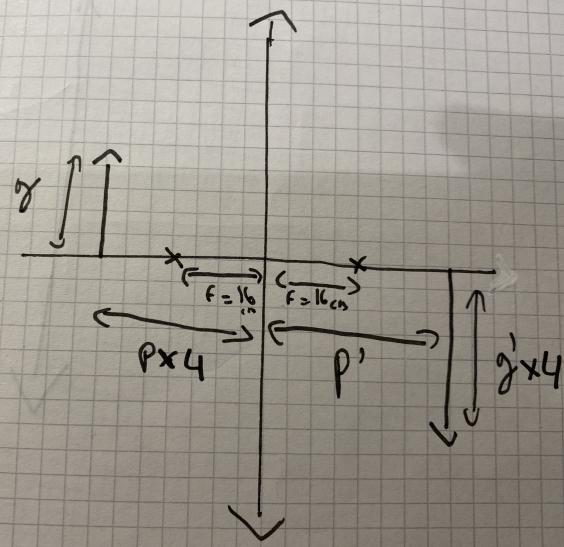
Tout d'abord, bravo Soph2341 pour avoir continué à chercher en attendant ma réponse  .
.
Tu as le bon raisonnement, il ne reste plus qu'à conclure  .
.
En fait, on a un système de 2 équations à 2 inconnues (P et P')  .
.
- relation de conjugaison: 1/f' = 1/p' - 1/p (petites fautes de frappe dans ton post  )
)
- Grossissement: p' = 4p
Je te laisse résoudre ce système d'équation et trouver ? 
Bonne chance,
Metal Oxalate
C'est bizzare dans mon cahier j'ai :
Loi des lentilles minces : 1/p + 1/p' = 1/f
Mais si je cherche sur internet je trouve 1/p - 1/p' =1/f'
Vous croyez que le faite que ce sois f' cela influence ?
Et du coup je comprend pas je mais deux fois la même égalité pour résoudre mon système :
1/f' = 1/p - 1/p' = 1/p x 4 - 1/p
Et je résous ensuite ou c'est un autre système ?
Et enfaite c'est vraiment pareille partout j'ai cette formule là et pas d'autres :
-> 1/f = 1/p + 1/p'
Dans mon cours , les feuilles du prof , etc
ce n'est pas une erreur de frappe de ma part ! C'est écris noir sur blanc sur le cour du prof
Je ne sais pas pourquoi c'est different ?
Concernant le choix de formule:
En fait, dans ma formule, f', p' et p sont des distances orientées (positive ou négative).
Ainsi: 1/f' = 1/p' - 1/p
Comme p est orienté dans le sens opposé à la lumière, p est négatif.
Ainsi, "-1/p" est positif  .
.
Peut-être que ta formule utilise les valeurs absolue, je ne sais pas.
Concernant l'exercice:
Oui, c'est ça il faut juste résoudre  .
.
1/f' = 1/p' - 1/p
1/f' = 1/(-4p) - 1/p = -5/(4p)
D'où: p = -5*f'/4
Je te laisse faire l'application numérique  .
.
Puis effectuer le même genre de raisonnement pour obtenir une image virtuelle (question B) 
Bonne nouvelle j'ai trouvé une explication satisfaisante et rassurante  .
.
Les deux formules sont correctes, mais la définition de p et de f est différente  .
.
Dans ma formule:
1/f' = 1/p' - 1/p
Les distances correspondent à la distance en partant du point O:
f' =OF' (positif comme F' est à droite de O)
p' = OP' (positif comme P' est à droite de O)
p = OP (négatif comme P est à gauche de O).
Alors que dans ta formule:
1/f = 1/p + 1/p'
Les distances correspondent sont différentes:
f =FO (et non pas OF !)
p' = OP' (positif comme P' est à droite de O)
p = PO (et non pas OP comme dans ma formule.) Comme PO = - OP, on retire le signe - 
Bef, tout va bien.
Tu peux utiliser la formule que tu souhaites (à condition de respecter les conventions de la notation choisie, bien sur  ).
).
Merci infiniment j'étais vraiment coincée pour cette exercice et j'ai enfin compris merci 
Je pourrais maintenant refaire le même genre d'exercices pour mon épreuve demain 
Je ferais attention de respecter les conventions de la notation 


