Bonsoir,

Énoncé :
Un enfant tire une luge à vitesse constante avec une force F faisant un angle ß (beta) par rapport au plan.
1/ Quelles sont les forces appliquées à la luge (frottements négliés). Quelle est la valeur de F ?
2/ Même question, les frottements sont représentés par une force f de valeur constante, colinéaire à la vitesse et de sens contraire.
3/ Déterminer dans les deux cas la valeur de Rn (réaction du support). Que devient cette valeur si les frottements augmentent ?



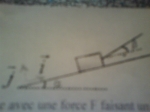
Voici le dessin, l'angle du bas, celui avec le support est α (alpha) et celui du haut, le fil avec la luge est ß (beta).

m = 6kg ; α (alpha) = 20° ;  ß (beta) = 15°  ;  f = 5 N   ;   g = 9.8 N.kg

Voilà mon problème, je trouve une valeur de F impossible (212.7 N).

Ce que j'ai fais :
P = mg = 6 x 9.8 = 58.8 N
Après application du principe d'inertie : P + Rn + F = 0

Après projection sur un repère (O;x;y)
De plus : Px = -P x sin α (alpha)      Py = -P x cos α
          Rnx= Rn     Rny = 0
          Fx = F x cos ß (beta)        Fy = F x sin ß (beta)



J'obtiens donc  :
   F x sin ß (beta) = P x cos α (alpha)
=> F x 0.26 = 58.8 x 0.94
=> F = 55.3 / 0.26 = 212.7 N


Par suite,
   Rn = P x sin α (alpha) - F x cos ß (beta)
=> 58.8 x 0.34 - 212.7 x 0.97 = -186.3

Voilà, je me pose la question suivante ?
Ai-je faux ? si oui, où ?

Ou
Est-il possible que Rn = |-186.3| = 186.3 N ??

Merci d'avance pour les réponses.