Inscription / Connexion Nouveau Sujet
Accueil l'île de la physique - chimie Forum de physique - chimieListe de tous les forums de physique - chimie LycéeOn parle exclusivement de physique/chimie, niveau lycée. TerminaleForum de terminale PhysiqueTopics traitant de Physique [tout]Lister tous les topics de physique - chimie
Niveau terminale
Partager :

Problème de physique : mécanique

Posté par
pfff 26-07-20 à 02:54

Bonjour, je bloque sur cet exercice. Merci de m'aider.

ÉNONCÉ

On considère le dispositif ci-dessous. ( Les parties 1 et 2 sont indépendantes )

1. Un solide supposé ponctuel de masse m = 200g, glisse le long de la ligne de plus grand pente AB d'un plan incliné faisant un angle = 30° avec le plan horizontal.

Le solide est abandonné en A sans vitesse initiale.

a- En considérant les frottements négligeables; déterminer l'accélération du centre d'inertie du solide.
En déduire l'équation horaire du mouvement.

b- Calculer la durée du parcours AB
Déterminer la vitesse V_B en B.

c- En réalité cette durée est égale à 1,3s. En admettant l'existence d'une force de frottement \vec{f} constante, opposé au vecteur vitesse.
Déterminer la valeur de cette force de frottement.

2. Le solide est maintenant lancé vers le point D et se déplace sur la piste ADEF. Les frottements sont négligeables sur les parties AD et EF de la piste.
Entre D et E, il existe des forces de frottements dont la résultante \vec{f} est de direction parallèle à DE et de valeur f = 0,9 N.

a- Le solide est lancé de A avec une vitesse V_A = 1m/s et atteint D à la vitesse V_D = 6m/s.
          -Déterminer la distance AH
          - En déduire l'angle dont est incliné la portion AD par rapport à
             l'horizontale

b- Le solide aborde la portion DE. Déterminer la vitesse V_E en E

c- Le solide s?arrête en M sur la portion de piste EF.
Déterminer l'angle , caractériser la position de M.

d- Déterminer l'expression de la réaction de la glissière en M.

e- Déterminer la vitesse minimale V_A_m_i_n que le solide doit posséder en A pour qu'il puisse atteindre F.

Données : AB = 2m , AD = L = 5m , DE = L' = 3m , OE = OF = r = 2m , g=10N/kg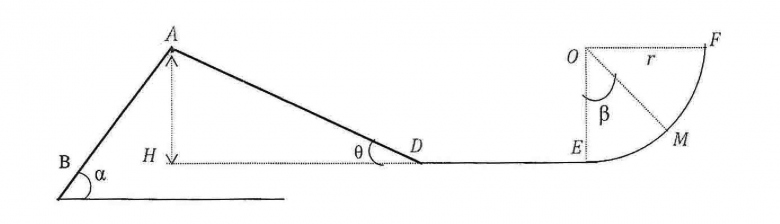


Problème de physique : mécanique


Mes réponses


1-Je trouve a = 5m/s² avec le théorème du centre d'inertie.

b J'ai d'abord cherché l'équation horaire du mouvement
x(t) = 2,5t²
x(t) = AB t = 0,89s.

J trouve V_b = 4,47m/s.

c- Je suis bloqué

***Titre complété pour plus de clarté***

Posté par
Vardyre : Problème de physique 26-07-20 à 07:39

Bonjour Pff ,
Pour la question C tu peux appliquer le Theorème de l'énergie cinétique entre A et B .

Posté par
pfffre : Problème de physique 26-07-20 à 07:55

Bonjour,
mais la vitesse V_b va changer vu que la durée du parcours à changer.

Posté par
pfffre : Problème de physique 26-07-20 à 08:02

voici comment j'ai essayé de faire. Vu que il ya présence de forces de frottement, la valeur de \vec{a} va changer donc :

d'après 1-b on a :  x(t) = AB \dfrac{1}{2}at² = AB
                                                            
                                                          
                                                                a = \dfrac{2AB}{t²}

avec la nouvelle valeur de t j'obtiens a = 2,37m/s²

j'ai ensuite appliqué le théorème du centre d'inertie entre A et B pour trouver f

Posté par
odbugt1re : Problème de physique 26-07-20 à 10:03

Bonjour,

Question 1.a et 1.b  :
Tes affirmations et calculs n'étant pas convenablement justifiés, je n'ai rien vérifié.

Question 1.c :
La méthode que tu utilises est correcte.

Posté par
pfffre : Problème de physique 26-07-20 à 10:20

Citation :
Tes affirmations et calculs n'étant pas convenablement justifiés, je n'ai rien vérifié.

D'accord

Citation :
La méthode que tu utilises est correcte.

D'accord


Je suis bloqué à la toute fin merci de m'aider

Posté par
odbugt1re : Problème de physique 26-07-20 à 10:22

De quelle "toute fin" est il question ici ?

Posté par
pfffre : Problème de physique 26-07-20 à 10:25

Citation :
e- Déterminer la vitesse minimale V_A_m_i_n que le solide doit posséder en A pour qu'il puisse atteindre F.

Posté par
odbugt1re : Problème de physique 26-07-20 à 10:37

Appliquer le théorème de l'énergie cinétique entre A et F

Posté par
pfffre : Problème de physique 26-07-20 à 10:55

Je calcule avec V_F = 0m/s ?

Posté par
pfffre : Problème de physique 26-07-20 à 11:08

\Delta EC = W(\vec{P}) + W(\vec{f}) + W(\vec{P}) + W(\vec{f}) + W(\vec{P})
  A-F         A-D                   A-D          D-E               D-E              E-F



\frac{1}{2}mv²_F - \frac{1}{2}mv²_A = mgH - f_1L + 0 - fL' - mgr


v_A = \sqrt{\dfrac{2}{m}(f_1L + fL') - 2gH + 2gr}


v_A = 6,52m/s


a quel moment V_amin intervient ?

Posté par
odbugt1re : Problème de physique 26-07-20 à 11:12

Pour que A atteigne F sa vitesse en ce point doit être supérieure ou égale à zéro.
Donc sa vitesse minimale doit être égale à zéro.

Posté par
pfffre : Problème de physique 26-07-20 à 11:22

D'accord

Posté par
odbugt1re : Problème de physique 26-07-20 à 11:28

Ton calcul est à revoir :
L'énoncé précise que les frottements sur AD sont négligeables.

Posté par
pfffre : Problème de physique 26-07-20 à 11:29

oui mais ,

Citation :
c- En réalité cette durée est égale à 1,3s. En admettant l'existence d'une force de frottement \vec{f} constante, opposé au vecteur vitesse.
Déterminer la valeur de cette force de frottement.

Posté par
odbugt1re : Problème de physique 26-07-20 à 11:44


Citation :
c- En réalité cette durée est égale à 1,3s. En admettant l'existence d'une force de frottement \vec{f} constante, opposé au vecteur vitesse.
Déterminer la valeur de cette force de frottement.


Tu mélanges le mouvement étudié à la question 1 sur la pente AB avec le mouvement étudié à la question 2 sur la piste ADEF

Posté par
pfffre : Problème de physique 26-07-20 à 11:57

Merci c'est vrai j'ai mélangé

\Delta EC = W(\vec{P}) + W(\vec{f}) + W(\vec{P}) + W(\vec{f}) + W(\vec{P})
  A-F         A-D                   A-D          D-E               D-E              E-F



\frac{1}{2}mv²_F - \frac{1}{2}mv²_A = mgH + 0 - fL' - mgr

Pour que A atteigne F sa vitesse en ce point doit être supérieure ou égale à zéro.
Donc sa vitesse minimale doit être égale à zéro.

v_A = \sqrt{\dfrac{2fL'}{m}-2gH + 2gr}


v_A =5,66 m/s

Posté par
pfffre : Problème de physique 26-07-20 à 12:01

Mince j'ai oublié d'enlever W(f)  dans la 1ere ligne mais dans la 2e ligne j'ai enlevé
                                                            A-D



\Delta EC = W(\vec{P}) +  W(\vec{P}) + W(\vec{f}) + W(\vec{P})
  A-F         A-D                 D-E             D-E              E-F



\frac{1}{2}mv²_F - \frac{1}{2}mv²_A = mgH + 0 - fL' - mgr

Pour que A atteigne F sa vitesse en ce point doit être supérieure ou égale à zéro.
Donc sa vitesse minimale doit être égale à zéro.

v_A = \sqrt{\dfrac{2fL'}{m}-2gH + 2gr}


v_A =5,66 m/s

Posté par
pfffre : Problème de physique 26-07-20 à 12:02

donc V_amin = 5,66 m/s

Posté par
odbugt1re : Problème de physique 26-07-20 à 12:07

Citation :


v_A = \sqrt{\dfrac{2fL'}{m}-2gH + 2gr}
v_A =5,66 m/s


Peut être ...
Je n'ai relevé que les erreurs visibles du premier coup d'œil.
Il y en a peut être d'autres que je ne rechercherais pas puisque tu ne te donnes pas la peine de détailler tes calculs.

Posté par
pfffre : Problème de physique 26-07-20 à 12:13

ok
De commencer à détailler à partir d'où ?

Posté par
odbugt1re : Problème de physique 26-07-20 à 12:14

Désolé.
J'ai zappé le détail de tes calculs.
Je trouve moi aussi VAmin = 5,66 m/s

Posté par
pfffre : Problème de physique 26-07-20 à 12:19

cool merci


Rechercher
Menu
Espace membre
Changer d'île
Mentions légales - Retrouvez cette page sur l'île de la physique - chimie
© digiSchool 2025

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 245 fiches de physique

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !