Inscription / Connexion Nouveau Sujet
Poulies
Bonjour/Bonsoir
J'ai besoin daide sur cet exercice
Merci d'avance
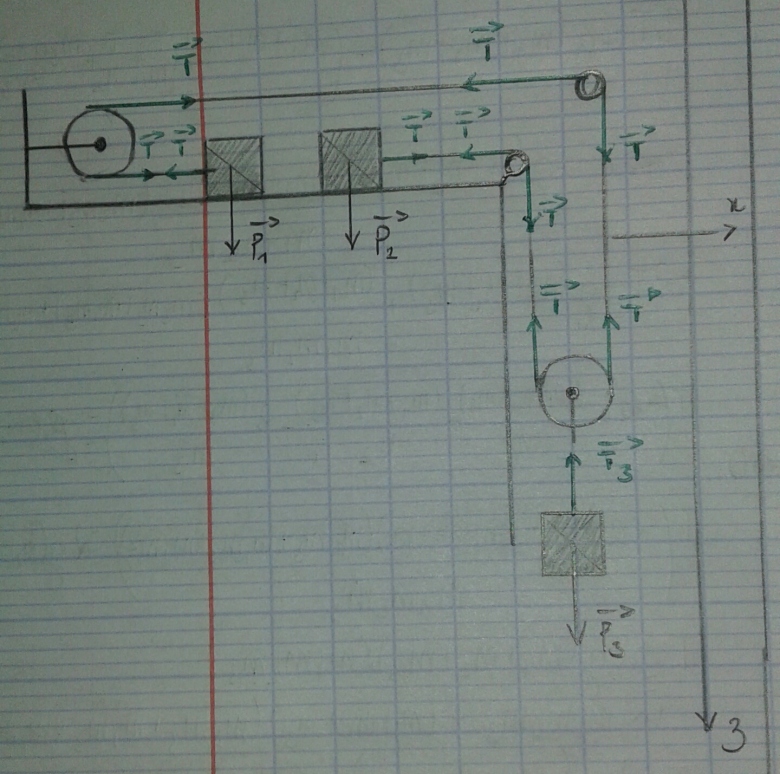
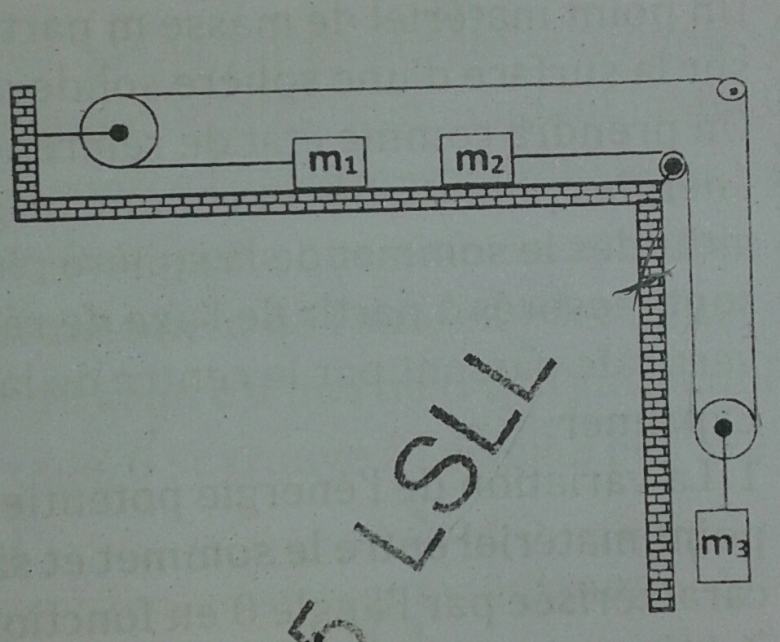
Trois corps de masse m1,m2 et m3 sont reliés par une corde de masse négligeable qui glisse sans frottements sur les gorges des poulies de masses négligeables.
Exprimer l'accélération de chacune des masses et la tension de la corde en fonction de m1,m2 et m3.
J'ai essayé de prendre pour système l'ensemble mais je n'arrive pas à avancer
Bonsoir
Tu peux isoler chacune des masses et leur appliquer le pfd
Ça te donnera 3 relations
Ensuite la longueur de la corde est constante donc il y a une relation supplementaire entre les déplacements des 3 masses
Voilà ce que j'ai fait
Système:S1
T=m1a1
Système:S2
T=m2a2
Système:S3
P3-T3=m3a3
T:tension de la corde
T3:tension du fil supportant la poulie d'en bas
Merci de me corriger
Oui quand je prend la poulie pour système j'ai
2T=T3
T3 c'est la tension du fil passant par le centre de la poulie de gauche
C'est que je n'arrive pas à insérer des schémas
C'est pas tres rigoureux, j'avoue 
En gros, Inextensible, de masse nulle, etc.
Donc la tension est la même partout.
Il manque la réaction du sol sur m1 et M2
La notation T un peu partout est abusive car les vecteurs n'ont pas tous la même direction
Il faudrait noter T1 , T2 etc. et après projection écrire
T1=T, T2=T etc.. en valeur algébrique
La corde a une longueur constante
Quand m1 bouge de x1 vers la gauche
Et M2 bouge vers la droite de x2
De combien descend m3 ?
Non
Quand m1 bouge de x1 vers la gauche
Et M2 bouge de x2 vers la droite
La longueur de corde horizontale diminue de x1+x2
D'autre part quand m3 descend de X3, alors la longueur de corde verticale (au dessus de m3) augmente de 2 x3 (car il y a 2 brins qui s'allongent)
Donc comme la corde garde la même longueur totale il faut que : x1+x2 = 2 x3
(A) T= m1 a1
(B) T= m2 a2
(C) m3 a3 = m3g - 2T = m3g - 2 m1 a1
(D) 2 a3 = a1+a2
Donc 2 a3= a1 + (m1/m2) a1
Et en reportant dans (C) tu trouves a1
Puis a2 etc.