Inscription / Connexion Nouveau Sujet
Physique: skieur sur pente avec frottements
Bonjour!
Voici l'énoncé d'un exercice de physique sur les vecteur-forces.
J'ai fait la majorité des questions mais ai quelques doutes sur les suivantes:
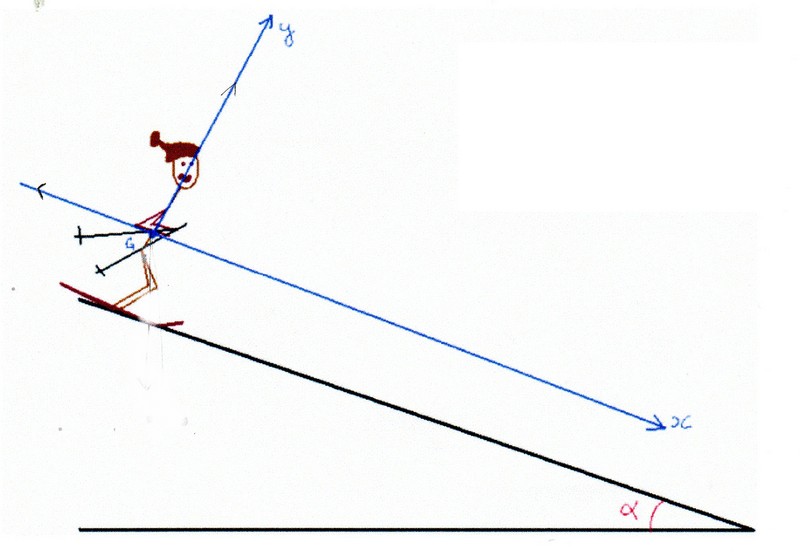
Un skieur de masse m=80kg glisse sur une pente enneigée (d'un angle alpha=18°).
Force de frottement notée f (opposée au déplacement du skieur). Vecteur représentant f est parallèle à la pente.
3.a) Déterminer les coordonnées des vecteurs forces dans la base choisie. (de centre : le centre de gravité, axe des abscisses suivant le mouvement du skieur, et axe des ordonnées vers le haut, même direction que force de réaction de la piste).
j'ai trouvée R(0; -Psinalpha) car, d'après la 1ère loi de Newton (on est dans les bonnes conditions), yR + O + yP = 0, donc yR=-yP=-Pcosalpha.
Mais ça ne devrait pas être négatif..si?
3.c) Déterminer par le calcul la valeur de la réaction normale du sol.
n'est-ce pas égal à R que l'on vient de calculer en 3.a) ?
Merci d'avance pour votre aide!
quelqu'un peut-il me dire si c'est normal que l'ordonnée de R soit négative alors qu'elle part du centre de gravité vers le haut (donc positif)?
Pour la question 3.a, voici ce que j'ai trouvé:
R (0 ; R)
F (-F ; 0)
P (x ; y)
avec R + F + P = 0 (chacun aves des flèches au-dessus).
P = m x g donc P = 80kg x 9,8 m/s² = 784 N.
donc x= P sinalpha = 242 N.
y= P cosalpha = 746N.
puisque les forces appliquées se compensent:
xR + xF + xP = O
- xF = -xP
xF = xP donc xF= P sinalpha.
de même pour yR:
yR + yF + yP = 0
yR = -yP donc yR = -P cosalpha.
Ma question est : pourquoi l'ordonnée de R est-elle négative, tandis que, dans la base choisie, le vecteur force représentant R part de l'origine vers le haut?
De nouveau un énoncé bancal.
Il est dit : "axe des ordonnées vers le haut, même direction que force de réaction de la piste."
Mais il y a des frottements, une partie due au frottement de la neige sur les ski et une partie due au frottement du skieur dans l'air.
La réaction du sol n'est donc pas perpendiculaire à la piste, cette réaction a une composante normale à la piste mais aussi une composante tangentielle due à la force de frottement neige-ski.
Je me demande si cela a même effleuré celui qui a donné ce problème.
De plus, il n'est pas spécifié si la vitesse de descente du skieur est ou non stabilisée ...
Cela fait beaucoup d'imprécisions (pour rester gentil) dans un même énoncé.
-----
3a)
En supposant l'axe des ordonnées du repère dans la direction et le sens de N (réaction normale du support) bien que ce ne soit pas la réaction totale du support à cause du frottement neige-ski.
P(mg.sin(18°) , - mg.cos(18°)), soit P(242 , -746) (attention au nombre de chiffres significatifs, normalement 2).
f(-|f| ; 0)
Remarque, on ne peut calculer |f| que si la vitesse de descente est stabilisée ou bien si l'accélération du skieur est connue au moment de l'évaluation.
Si la vitesse est stabilisée (ce qui n'est pas précisé dans l'énoncé), alors |f| = 242 N et donc f(-242 ; 0)
(attention au nombre de chiffres significatifs, normalement 2).
---
3c)
|N| = mg.cos(18°) = 80 * 9,81 * cos(18°) = 746 N
N(0 ; 746) (à arrondir à 2 chiffres significatifs).
-----
Sauf distraction et avec toutes les suppositions qui ont du être faites suite à un énoncé non précis.

Ce n'est pas de la faute de l'énoncé, c'est moi qui ai ommis de préciser certaines données.
Le mouvement du skieur est rectiligine et uniforme, donc la vitesse et stabilisée.
On ne prend en compte qu'une seule force de frottement pour le système (skieur et skis).
Mais les résultats que j'ai trouvé sont donc justes alors..?
Quelle est l'unité de la norme?
MERCI BEAUCOUP!!!
Effectivement, l'axe des ordonnées n'est pas perpendiculaire à l'axe des abscisses.
Comme calculer alors les coordonnées du vecteur Poids, si on ne peut utilisier ni cos alpha ni sin alpha (n'étant pas dans un triangle rectangle)?
Quelqu'un peut-il me répondre?
Bonjour,
J'aimerais supprimer l'image du seul post que j'ai publié sur l'île.
Merci d'avance pour votre efficacité, et bravo pour votre site!
*** message déplacé ***