Inscription / Connexion Nouveau Sujet
PHYSIQUE: Rotation d'un solide soumis à trois forces.
Bonsoir à tous , veuillez m'aider s'il vous plaît.
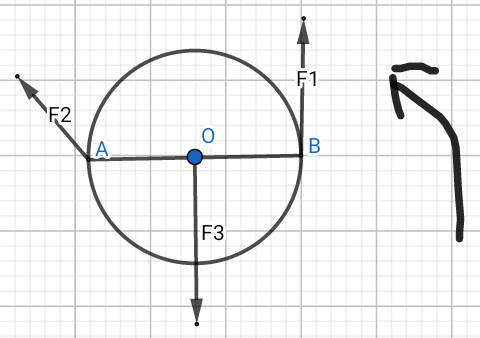
Un disque de rayon r=OA=OB=20cm , en mouvement de rotation , effectue 5 tours en 1 minute.
Durant le mouvement , il subit les actions des force contenues dans le plan vertical de la figure , telles que :
qui a pour intensité 5N , est perpendiculaire au rayon OB;
qui a pour intensité 3N , fait un angle de 60° avec le vecteur
;
qui a pour intensité 5N , passe par le point O , centre de symétrie du disque où passe l'axe de rotation perpendiculaire au plan de la figure .
1) Calcule le travail effectué par chacune de ces trois forces pendant tout le mouvement .
2) Calcule la puissance de chacune de ces forces .
Bonjour
Il faut calculer le moment de chacune de ces forces par rapport à l'axe de rotation. Uu obtiens ensuite le travail en multipliant le moment par l'angle de rotation mesuré en radians.
Bonsoir , 20cm = 0,2m
F1 est du même sens que le sens du mouvement choisit donc
M(F1)= + F ×OB
M(F1)= 5×0,2=1N.m
F2 est aussi du même sens que le sens du mouvement choisit donc
M(F2) = +F2×OA= 3×0,2=0,6N.m
F3 est du sens contraire ...
Donc M(F3)=-5×0,2=-1 N.m
Je calcule leurs travaux .
On sait que W(F)=M(F)×w avec ( W(F) :travail de la force F , w(oméga): vitesse angulaire ).
or w= r×s , on a : r=20cm= 0,2m et s est l'abscisse angulaire =60°
* je calcule w pour F1 .
w= r× 90° car est perpendiculaire à
w= r×π/2 car 90° en radian =π/2
Donc w= 0,2×π/2= 0,31 rad /s
* pour F2
w=r× 60° ( dans l'énoncé ).
w= 0,2×π/3 car 60° en rad = π/3
w= 0,2 rad/s
* Pour F3
Même chose que F1 car F3 est perpendiculaire OB.
Donc w=0,31rad/s.
• Leurs travaux maintenant.
- Pour F1 .
W(F1) = M(F1) ×w = 1×0,31=0,31 J
- Pour F2.
W(F2)=M(F2)×w
=0,6×0,2=0,12J
- Pour F3
W(F3)= M(F3)×w
= -1×0,31=-0,31 J.
OK pour le moment de F1
Pour F2 :quelle est la distance entre l'axe de rotation et la ligne d'action de la force ? Ce n'est pas R... Il faut tenir compte de l'angle de 60° dont parle l'énoncé. Ensuite : cette force favorise la rotation dans le sens positif ou s'y oppose ?
Pour F3 : quelle est la distance entre l'axe de rotation et la ligne d'action de la force ? Ce n'est pas R... Le résultat est simplissime...
Je pense que tu n'as pas vraiment compris comment calculer le moment d'une force par rapport à un axe de rotation. Tu as retenu une seule formule et cette formule ne s'applique que dans des cas très particuliers comme le cas ici de F1. Il te faut revoir ton cours sérieusement.
Le document ci-dessous pourra peut-être t'aider ; on y trouve les différents cas illustrés de schémas très clairs :
![]()
Mon message de 17h59 ne tient pas compte de ton message de 18h00.
Pour la suite, tu confonds travail et puissance. Pour le travail, le moment doit être multiplié par l'angle de rotation mesuré en radians. Pour la puissance, c'est la vitesse angulaire qui intervient.
Ah d'accord , mais je ne vois pas les données de la correction du premier exo sur le lien que vous avez partagé .
Du coup j'en profite pour que vous vérifiez ce que j'ai fait .
Pour le a) d = 0,2×sin (45°)=0,14m
b) M∆(F)=F×d×sin (F;d)=400×0,2×1=80N.m
Concernant le moment de F2 :
Le bras de levier (voir document joint) vaut R.sin(60°) : complète le schéma pour t'en convaincre. Je ne vois pas ce qu'un angle de 45° vient faire ici. D'autre part, comme déjà dit, cette force tend à faire tourner le disque dans le sens négatif...
Concernant le moment de F2 :
Le bras de levier (voir document joint) vaut R.sin(60°) : complète le schéma pour t'en convaincre. Je ne vois pas ce qu'un angle de 45° vient faire ici. D'autre part, comme déjà dit, cette force tend à faire tourner le disque dans le sens négatif...
Et M(F3)=-F3×r×sin90°=1N.m
Essaie de mettre en mouvement une porte entre-ouverte en exerçant une force au niveau de la ligne des gonds (axe de rotation) : la porte va-t-elle bouger ? Tu as étudié en cours que la notion de moment de force par rapport à un axe de rotation sert à mesurer l'influence de cette force sur la rotation du solide autour de l'axe de rotation. Lorsque la ligne d'action de la force passe par l'axe de rotation le moment est nul :
M(F3) = 0
Je ne sais pas si tu es habitué à algébriser les moments. Puisque F2 tend à faire tourner le disque dans le sens négatif, il est préférable d'écrire :
M(F2)=-F2.OA.sin(60°)
Ah d'accord monsieur .
J'ai une question qui va vous sembler un peu bête .
Quand est ce qu'on utilise sin et cos en physique ?
Ce n'est pas le bon argument : si on modifie la direction de la force F3 tout en maintenant sa ligne d'action passant par l'axe de rotation, on obtient toujours un moment nul. C'est le bras de levier qui ici est nul.
Les travaux.
Pour F1
W(F1)=M(F1)×w=1×r×60°=12 J
W(F2)= M(F2)×w=-0,52×r×60°=-6,24J
W(F3) = 0J car M(F3)=0N.m
Mon message de 17h59 ne tient pas compte de ton message de 18h00.
Pour la suite, tu confonds travail et puissance. Pour le travail, le moment doit être multiplié par l'angle de rotation mesuré en radians. Pour la puissance, c'est la vitesse angulaire qui intervient.
Oui pour ton dernier message. Pour le travail et la puissance, tu commets exactement les mêmes erreurs que dans ton autre message. Les explications fournies par odbugt1 dans son message du 30-11-19 à 21:44 sont pourtant parfaitement claires !
Le problème ici c'est que on nous dis dans l'énoncé 5 tours en 1 minute .
Si c'était 5 tours par minute , on pouvait poser 1 tour =2π donc 5×2π=10π et ensuite 1 min = 60s donc 5tours /min = 2π/60s=0,104rad /s , ce qui serait plus simplisme.
Puisqu'une rotation de N=5 tours correspond à un angle de rotation du solide :
 =2
=2 .N=10
.N=10 rad, il suffit de multiplier chaque moment déjà calculé par
rad, il suffit de multiplier chaque moment déjà calculé par  pour avoir le travail W en joules.
pour avoir le travail W en joules.
W=M(F).
Tu obtiens ensuite la puissance en divisant ce travail par la durée du mouvement :  t=60s.
t=60s.
P est alors mesurée en watts.
effectue 5 tours en 1 minute
Il s'agit d'un extrait de la première phrase de ton énoncé...
Je t'ai fourni les relations permettant de déterminer le travail et la puissance pour une force F quelconque appliquée au disque en rotation. Il faut appliquer ces formules générales à F1, puis à F2 puis à F3 : relis bien l'énoncé :
1) Calcule le travail effectué par chacune de ces trois forces pendant tout le mouvement .
2) Calcule la puissance de chacune de ces forces .
Il faut bien lire et bien comprendre l'énoncé...