Inscription / Connexion Nouveau Sujet
physique Kepler
bonjour ,
énonce
On a un satellite de masse m en orbite
avec une distance R du centre de la Terre avec une période T.
On ajoute un second satellite de masse 2m orbitant à une distance 2R du centre de la Terre.
on cherche la période de révolution T' du satellite
resolution :
j'ai utiliser la 3 loi de kepler
on veut trouvé T'
on commence par T²=T' ?
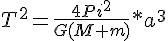
T² = 4Pi²/(G(M+m)) * R³
T'² = 4Pi²/(G(M+2m)) * (2R)³
T'²/T² = (M+m)/(M+2m) * 2³
T'²/T² = 8*(M+m)/(M+2m)
T'² = T² * 8*(M+m)/(M+2m)
Et comme M > > > m, on a : et donc :
Sauf distraction. 
Merci j'ai revu votre raisonnement il est parfait !
par contre j'ai deux question :
- pourquoi (M+m) / ( M+ 2m ) = 1 ?
- aussi , vous avez posez R=2 ? que vous avez mit au cube après
LB
(M+m)/(M+2m)
= (M+2m-m)/(M+2m)
= 1 - m/(M+2m)
Et donc comme M > > m, on a
-----
Exemple numérique :
M = 6.10^24 kg (masse de la Terre) et m < < < M
Pour fixer mes idées, les satellite artificiels les plus massifs jusqu'à ce jour font 20 tonnes.
Si on considère (par exemple) que le plus massif des satellites fait 20 tonnes --> 2m = 20000 kg et n = 10000 kg
(M+m)/(M+2m) = 1 - m/(M+2m) = 1 - 10000/(6.10^24 + 20000) = 1 - 1,67.10^-21
(M+m)/(M+2m) = 1 - 0,00000000000000000000167
(M+m)/(M+2m) = 0,99999999999999999999833
Soit donc
-----
aussi , vous avez posez R=2 ? que vous avez mit au cube après
Je n'ai pas fait cela.
En faisant le rapport T'²/T², les R³ contenus dans T'² et T² se simplifient.
Le 2³ qui subsiste dans le rapport T'²/T² provient de (2R)³/(R³) = 2³.R³/R³ = 2³



