Inscription / Connexion Nouveau Sujet
Peut-on voir le drapeau USA sur la Lune depuis la Terre ?
Bonjour à vous, voici l'énoncé de mon exercice :
Une étoile ponctuelle, c'est-à-dire assez lointaine pour être en forme de point, est diffractée par l'ouverture du télescope. Cela est de même pour une étoile double. Le plus petit détail (angle) perceptible par un télescope est donnée par la relation suivante :
= 1.22 . 
/ a
Où a est le diamètre du télescope.
La Lune étant à 380 000 kilomètres de la Terre, avec un télescope de 10 mètres de diamètres, peut-on voir le drapeau planté sur la Lune par la mission Apollo XI ? Quel serait la taille du plus petit objet que l'ont peut distinguer ?
Je sèche sur ce problème depuis au moins une heure. Je suis parti du principe que a = 10 mètres, donc j'en ai conclu que :
= 0,122 .
Problème : je ne connais pas . J'ai cherché sur internet une valeur possible qu'on pourrait utiliser, mais il n'y a pas de longueur d'onde de la lumière, et c'est ça qui m'embête.
Je n'ai pas appris les "secondes d'arcs", donc pouvez-vous m'aider en ne parlant pas de cela s'il vous plaît ? Je suis en Terminale.
Et aussi, est-ce possible que vous ne donniez pas la réponse ? J'aimerais juste qu'on m'aiguille sur cela, et trouver la réponse par moi-même si vous voyez ce que je veux dire.
Bonne soirée !
Re-bonsoir, j'ai oublié de préciser que j'ai également essayé de remplacer par la distance Terre-Lune, ce qui me donne 8,36 . 107 mètres, mais je ne saurais dire ce que cela veut dire, et je pense que c'est faux étant donné que la longueur d'onde ne peut pas être égal à une distance.
Donc j'ai essayé de calculer en utilisant la formule :
= c / t
c est la vitesse de la lumière dans le vide, qui est 3 . 108 mètres par secondes, et t serait donc le temps que met la lumière pour faire le trajet Terre-Lune, qui est d'environ 1.28 secondes.
(Calcul : t = d / v, donc t = 3,8 * 108 / 3 . 108 où d est la distance Terre-Lune en mètres, et v la vitesse de la lumière dans le vide en mètres par secondes, d'où t = 1.28 secondes).
Ainsi, on a t = 1.28 et c = 3 . 108 . On peut donc faire le calcul suivant :
= 3 . 108 / 1.28 ce qui nous donne donc = 234 375 000 mètres.
L'équation devient :
= 0.122 . 234 375 000
Ou encore 
2 859 375 mètres, ou encore 2 859,375 kilomètres.
Par conséquent, la taille du plus petit objet que l'on peut distinguer devrait donc être égal à 2 859,375 kilomètres, d'où le drapeau américain ne peut pas être vu par un téléscope de 10 mètres de diamètre.
Le truc c'est que je ne suis pas du tout sûr de ma réponse :/ Est-ce bien ça ? Ou me suis-je trompé quelque part ?
Hello
Ou me suis-je trompé quelque part ?
Un peu partout en fait ...
(bon, tu me diras, il était très tard
Donc, l'angle limite sous lequel on ne peut distinguer le drapeau est
où
est la LONGUEUR d'ONDE
Considère donc que le drapeau émet dans l'intervalle de longueur d'onde [400 nm, 800 nm]
Je te laisse proposer un raisonnement maintenant: utiliser le rouge? le bleu? le violet contenu dans le blanc?
Ici on devrait prendre les 2 longueurs d'ondes 400 nm et 800 nm pour faire une intervalle, non ?
Donc on devrait prendre 400 nanomètres, et ça donne donc (après conversions), 4,88 . 10-8 radians (et non mètres ?). Si on prend 800 nanomètres, alors le résultat est de 9,76 . 10-8 radians. On peut donc dire que la taille du plus petit objet visible depuis la Terre est compris entre 9,76 . 10-8 radians et 4,88 . 10-8 radians. Mais je pense qu'il faut trouver un résultat en mètres, encore une fois je me suis peut-être trompé.
Je suis un peu nul en physique, donc j'essaie mais voilà x))
Bon, on progresse (c'est avec des petits pas que l'homme fait de grands bonds pour l'humanité )
Supposons que l'angle soit = 5.10-8 rad
On va essayer de résoudre le problème en se posant la question: quelle devrait être la dimension du drapeau (longueur d) pour qu'on puisse le voir sous cet angle depuis la Terre située à D = 380 000 km
(n'oublie pas que Pythagore est ton ami)
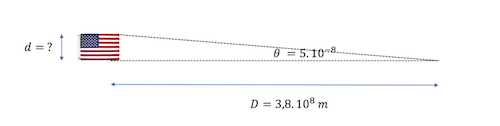
Le triangle est rectangle mais on ne connaît qu'une mesure. On pourrait utiliser alors le cosinus de l'angle pour ensuite trouver d en utilisant Pythagore, mais pourquoi ne pas utiliser la tangente alors ?
Ouais c'est ce que je pensais du coup :
d = D x tan()
==> d 3,8 . 108 . 5 . 10-8
Donc d 3,8 . 5 19 d
La longueur d vaut donc environ 19 mètres ? On a pris en radians, je ne sais pas si c'est bon ou pas.
Ah oui vrai, car cette expression est vraie pour les petits angles en radians. Du coup ceci est vrai, et la longueur du plus petit objet que l'on peut distinguer avec un télescope de 10 mètres vaut 19 mètres, d'où le drapeau américain ne peut pas être vu depuis la Terre. C'est bien ça ?
Tout à fait (19 m c'est plus un drapeau, c'est une bâche de court de tennis, et en plus il faudrait qu'elle soit violette, les russes et leur drapeau rouge aurait eu besoin d'un drapeau de plus de 30 m)
Annuler
connectez vous