Inscription / Connexion Nouveau Sujet
Pendule simple
Bonjour tout le monde, veuillez m'aider svp.
Problème
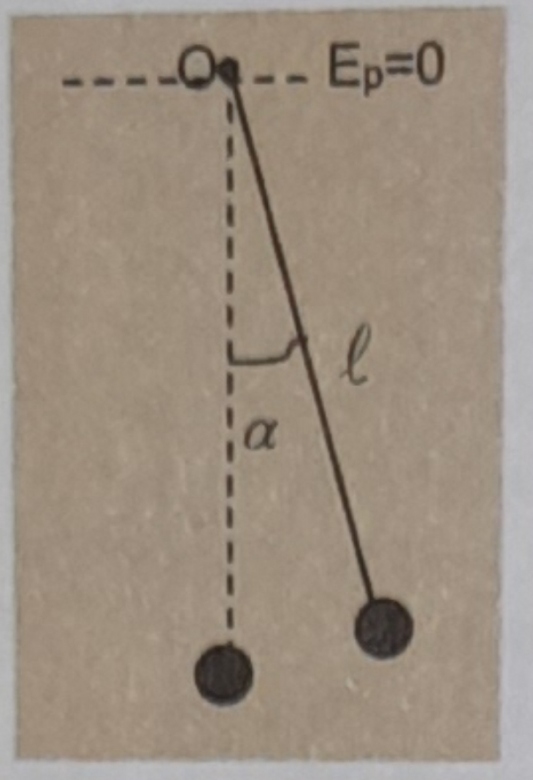
Un pendule simple est constitué par un fil de masse négligeable de longueur l portant une bille très dense de masse m assimilable à un point. Le fil est fixé en O. On écarte le fil de sa position d'équilibre d'un angle puis on l'abandonne sans vitesse.
1) À une date t, le fil fait avec la verticale un angle 
, la vitesse de la bille est v.
Écrire l'expression de l'énergie mécanique du pendule dans le champ de pesanteur.
On adoptera comme référence pour l'énergie de pesanteur le plan horizontal passant par O.
2) On envisage le cas où l'amplitude des oscillations est faible.
a) Établir l'équation différentielle du mouvement du pendule.
b) Calculer la période des oscillations.
c) Écrire l'équation horaire.
On donne l = 50 cm ; g = 9,8 m/s² ; m = 6⁰
La date 0 est l'instant où le pendule passe par la verticale en allant dans le sens positif.
3) Quelle serait la nouvelle période du pendule si sa longueur augmentait de 1/100 de sa valeur initiale ?
1) Expression de l'énergie mécanique
Par définition : Em = Ec + Ep = ½mv² + mgh
Maintenant, je ne sais pas si je dois faire un dessin puis exprimer la hauteur h, ou alors si je dois laisser l'Em en fonction de h.
Je pense que tu dois exprimer l'énergie potentielle de pesanteur en fonction de m.g.l et de l'angle en tenant compte du niveau d'altitude nulle imposé par l'énoncé et rappelé sur le schéma.
Donc Em = ½mv² - mgh = ½mv² - mgl.cos
Je demande aussi je vais chercher l'expression de v² puis remplacer dans l'Em. C'est ça ?
Ce que tu as écrit est bien l'équation demandée. Tu peux aussi écrire que cette constante est la valeur de l'énergie mécanique à l'instant de date t= 0, lorsque le pendule est abandonné à lui-même.
2.a) Équation différentielle du mouvement
Comme l'Em = constante, sa dérivée par au temps est nulle.
Donc : ½m.2v'v + mgl.'.sin = 0
Or v' = '' et v = '
Alors ''.' + gl.'.sin = 0
D'où '' + gl.sin = 0 est l'équation différentielle du mouvement.
C'est ça ?
Raisonnement correct, mais une erreur sur la relation entre vitesse et vitesse angulaire :
v=l.'
v'=l."
Ensuite, puisque l'énoncé précise que les angles restent faibles (pas plus de 6°), tu peux poser pour simplifier :
sin()
Tu obtiens alors une équation différentielle dont la résolution est simple.
vanoise, je te remercie beaucoup.
2.b) Période des oscillations
Par définition T = 2
/
Or ² = g/l (d'après l'équation différentielle)
Donc T = 2/
(g/l)
Alors T = 2.(l/g)
Oh je me rappelle bien de cette relation !
AN : T 1,42 s
Bien.
2.c) Équation horaire
L'équation horaire est la solution de L'équation différentielle précédente. C'est une Équation de la forme = m.cos(t + 
)
Or, la date 0 est l'instant où le pendule passe par la verticale en allant dans le sens positif, donc = 0⁰
Alors 0 = m.cos 
cos = 0 = 
/2
Et m = 6⁰ = /30 rad
D'où = /30.cos(0,226t /2)
C'est bon ?
Ce que tu as fait est correct mais il est possible de lever l'indétermination sur la phase initiale en raisonnant sur le signe de la vitesse initiale.
Donc ' = d/dt = -m.sin(t + )
Or à t = 0, ' est max et vaut ' = m.
Alors : sin = - 1
Or : cos = 0 (déjà établi ci-haut)
Donc si je comprend bien : = - /2 rad
D'où = /30.cos(0,226t - /2)
C'est ça ?
D'accord
donc : = 0,1.sin (0,226t) (en rad)
Question 3) calcul de la nouvelle période T'
T' = 2(l'/g)
Où l' = l + l.1/100 = 1,01.l = 1,01*0,5 = 0,505 m est la nouvelle longueur du pendule simple.
AN : T' 1,45 s
On attend une bonne précision dans l'application numérique ici. Cela peut se faire directement à la calculatrice numérique à condition de ne pas arrondir les calculs intermédiaires. On peut aussi présenter littéralement les choses. En notant 
l l'augmentation de longueur, la nouvelle période est :
alors que :
le rapport des périodes vaut :
on fait ainsi apparaître l'allongement relatif :
Cela ne conduit pas tout à fait à ton résultat.
PS : sachant que :
; ce qui conduit à T'
1,005T... L'écart est très faible, ce qui rend cette question peu cohérente dans la mesure où l'énoncé demande d'arrondir g à 9,8m/s2...
D'accord, mais j'ai commis une erreur dans l'application numérique. Nous obtenons la même valeur pour T'
T' 1,43 s
Annuler
connectez vous