Précision : dans le livre où j'ai pris l'exercice, la valeur de C est : C = 0 50Nm/rad. C'est comme ça ils ont écrit.
Et moi, j'ai pris C = 0,50 Nm/rad en estimant que c'est une erreur de leur part.

Maintenant, ce que je n'ai pas du tout compris, c'est le rôle de ce ressort ici, afin de pouvoir mieux interpréter et faire un bon schéma.

Bonsoir
Tu as déjà eu l'occasion d'exprimer l'énergie potentielle de pesanteur d'un pendule. Tu dois aussi connaître l'expression de l'énergie potentielle élastique d'un ressort spirale...
Contrairement à un dispositif que tu as récemment étudié, le poids et le ressort exercent tous deux des actions de rappel, c'est à dire des actions qui tendent à ramener le pendule vers sa position d'équilibre. Cela doit se traduire au niveau des signes...

D'accord.

E_m = E_c + E_pp + E_pe

• E_c = ½J'²  (énergie cinétique de rotation du pendule) et J = ⅓m(2L)²
Donc E_c = ½(⅓m.4L²).'² = (4/6)mL².'²

• E_pp = mgh est l'énergie potentielle de pesanteur
• E_pe = ½C² est l'énergie potentielle élastique du ressort.

Maintenant je dois faire un dessin avec un bon paramétrage, puis déterminer la hauteur h.

C'est ça ?

Il te faut faire un schéma du dispositif avec une élongation angulaire quelconque  et expliciter "h" en fonction de L et de .
Même si la formule que tu vas obtenir est valide en valeur algébrique, donc pour un signe de quelconque, tu as toujours intérêt à faire une figure avec >0 ; les risques d'erreurs de signe sont plus faibles.

Bonjour vanoise, bonjour tout le monde. Je me suis absenté trop longtemps. J'étais très occupé par autres choses.

Continuons !

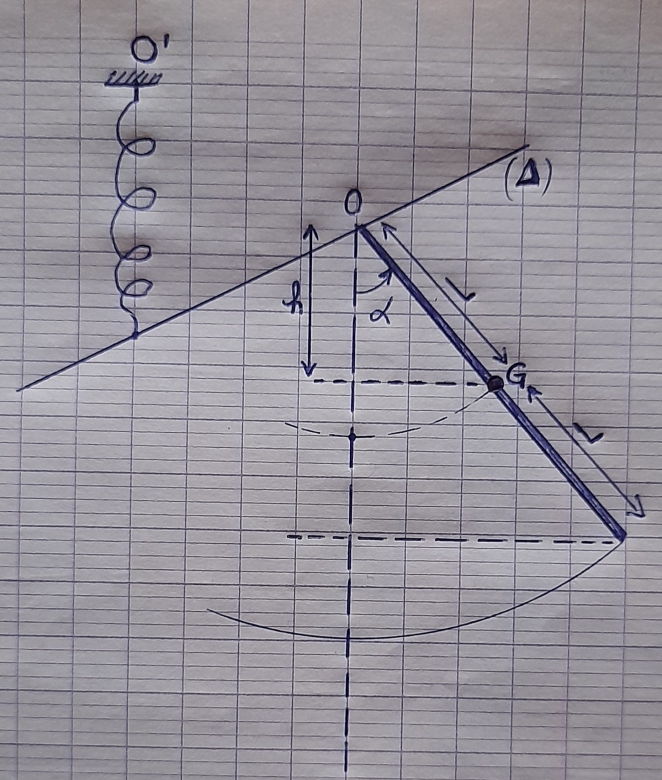
Voici le schéma que j'ai proposé avec le paramétrage de "h" suivant. G est le centre d'inertie de la tige homogène (G est au milieu de celle-ci).
Donc h = L.sin

Or selon l'énoncé, l'énergie potentielle est nulle lorsque le système est l'équilibre, c'est-à-dire au moment où la tige est verticale (=0⁰). "h" est au-dessus du niveau de référence, donc E_pp = +mgh E_pp = mgL.sin

Alors E_m = (4/6)mL².'² + mgL.sin + ½C²

C'est ça ?

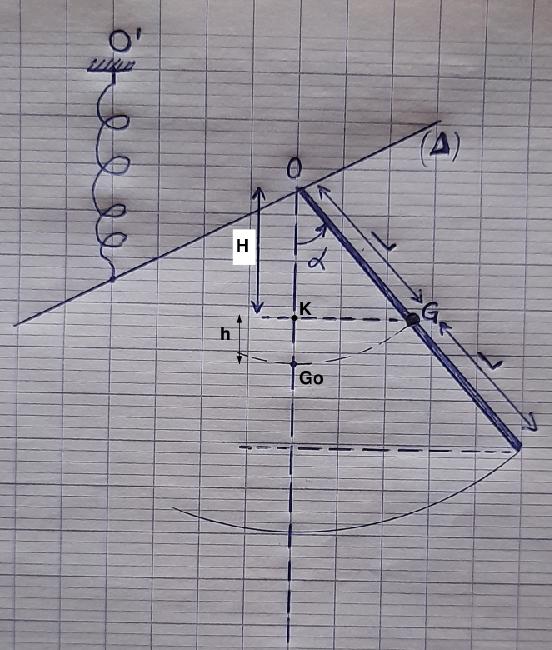
Quelques remarques sur ta figure :
1°) : Le ressort est un ressort spiral exerçant un couple de rappel ;
2°) : La distance que tu appelles "h" et qui représente la distance (OK) de la figure ci-dessous ne vaut pas L.sin(). Je préfère la noter "H".
3°) : selon l'énoncé, l'altitude nulle est celle de la position d'équilibre de G, notée G_o sur la figure ci-dessous. L'énergie potentielle de pesanteur s'écrit dans ces conditions :
E_pp=m.g.h avec h=G_oK, distance que je te laisse exprimer en fonction de L et de cos().

D'accord
h = G₀K = L(1-cos)
Donc E_pp = mgL(1-cos)
Le ressort exerce un couple de rappel, donc
E_pe = - ½C²
Alors l'E_m devient :
E_m = (4/6)mL²'² +mgL(1-cos) - ½C²

Question : est-ce que je pouvais travailler avec mon paramétrage de "H" ?

h=L-H...
En choisissant la position d'énergie potentielle de pesanteur nulle en =/2 on aurait obtenu : E_pp=-m.g.H=-m.g.L.cos() ; tu peux remarquer que cette expression ne diffère de celle demandée que d'une constante...
Ton expression de E_pp est correcte. Le ressort spiral exerce un couple de rappel car le moment du couple qu'il exerce sur le pendule tend constamment à ramener celui-ci vers sa position d'équilibre correspondant à =0 ; son moment par rapport à l'axe de rotation vaut (-C.). Justement à cause de ce signe "-" dans l'expression du moment, l'énergie élastique correspondante est toujours positive :

On peut parler de la démonstration si tu le souhaites mais je ne suis pas sûr que celle-ci soit à ton programme...

Par convention, la variation d'énergie potentielle est égale à l'opposé du travail :
dE_pe=-W
Pour une rotation élémentaire telle que l'élongation angulaire passe de à (+d), le travail élémentaire est égal au produit de la rotation élémentaire par le moment du couple :
W=M.d=-C..d
Ces deux relations conduisent à l'expression de la dérivée de l'énergie potentielle par rapport à l'élongation angulaire :



Il n'y a plus qu'à passer aux primitives en choisissant arbitrairement : E_pe=0 si =0.

D'accord, j'ai compris.
L'énergie mécanique est alors :
E_m = (4/6)mL²'² + mgL(1-cos) + ½C²

2) Équation différentielle du mouvement
Je dérive l'énergie mécanique puis j'égalise à zéro.
J'obtiens :
⅔mL²".' + mgL.'.sin + ½C'. = 0

Je simplifie partout par ', puis j'ordonne, sachant que sin

⅔mL²" + mgL. + ½C. = 0

⅔mL²" + (mgL +  ½C) = 0

Ta méthode générale est bonne mais deux petites erreurs ou étourderie de math :
les dérivées par rapport à t de ² et de '² sont respectivement :
2.' et 2'." .

OK je vois.

Je trouve alors " + ¾[g/L + C/(mL²)] = 0

Ici la dérivée de l'E_m est nulle, parce qu'elle une constante. Comment justifier que E_m = constante ?
Je constate à chaque fois qu'on demande d'Établir une Équation différentielle à partir de l'E_m, on la considère comme une constante.

L'énergie mécanique se conserve en absence de frottement : on néglige ici les forces de frottement exercées par l'air sur les parties mobiles et les frottements au niveau de l'axe de rotation.

Si mon équation différentielle est correcte, alors la période des oscillations est :

L'équation différentielle est de la forme :
" + ₀². = 0

Par identification, J'obtiens :

Sachant T₀ = 2/₀

Je trouve

AN : m = 300 g ; L = 20 cm ; C = 0,50 Nm/rad
J'ai utilisé g = 10 m/s²

Je trouve T₀ = 0,49 s

OK pour le résultat littéral. Je n'ai pas la même valeur numérique que toi.
PS : Il est intéressant d'arrondir g à 10m/s² quand il s'agit d'obtenir "de tête" un ordre de grandeur mais, quand on dispose d'une calculatrice scientifique, pourquoi introduire volontairement 2% d'erreur ?

D'accord, en prenant g = 9,8 m/s² et avec la calculatrice, je trouve
T₀ = 0,76 s

D'accord avec toi maintenant !

Merci vanoise.
Si quelqu'un a des fiches de cours sur le stroboscope, les mouvements vibratoires, propagation d'un signal, les différents types de signaux..., prière de m'aider svp.