Inscription / Connexion Nouveau Sujet
Pendule élastique
Merci d'avance
j ai trouver un petit problème lorsque je suis entrain d'étudier un pendule élastique énergitiqument
1) trouver à instant t l expression de l énergie potentielle Ep = Epp +Epe en fonction de x est k
Puis déduire l énergie mécanique
Epp(0)=0 le plan horizontal auquel appartient G
Epe(0)=0 l état ou le ressort est allongé à l'équilibre
Je fait appliquer le 1 loi de Newton à l'équilibre je trouve
Et on a :
D'où
Mais pour Epp je ne sais pa comment trouver
Bonjour
Le choix du niveau d'énergie potentielle élastique nulle n'est pas judicieux.Il est préférable de le choisir lorsque le ressort est au repos. Si lo est la longueur à vide, et "l" la longueur à un instant quelconque, l'expression générale de l'énergie potentielle élastique est ainsi :
Epe=½k(l-lo)2
Dans le cas particulier de l'équilibre, on peut noter 
l l'allongement (l-lo), l'allongement à un instant quelconque au cours du mouvement est ainsi 
l+x).
Je te laisse étudier le cas particulier de l'équilibre ; tu vas en déduire une relation simple entre k.l m,g et 
.
Cela permettra de simplifier l'expression de Ep dans le cas général.
: mettre un ":" suivi d'une "(" génère ce smiley qui n'a pas de sens ici. A l'avant dernier paragraphe, il faut lire :
"l'allongement à un instant quelconque au cours du mouvement est ainsi : (l+x)."
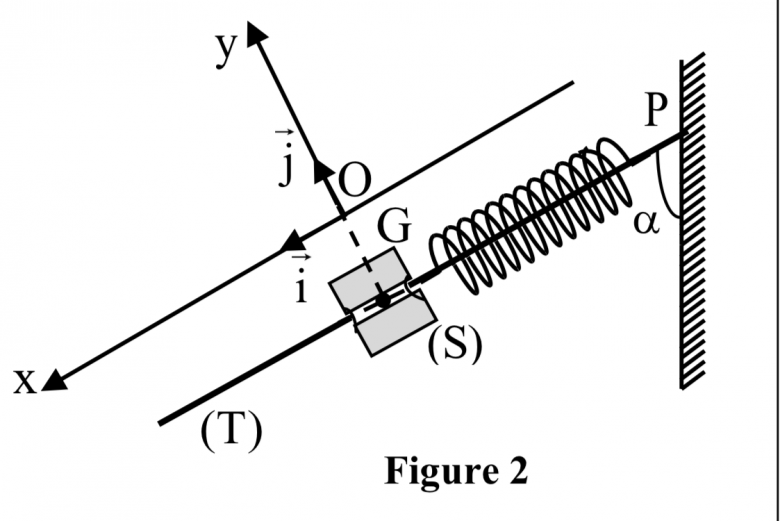
Pour l'énergie potentielle de pesanteur : tu sais qu'elle est nulle en x= 0. Suppose maintenant x>0 : quelle est l'altitude de G dans ce cas, le niveau d'altitude nulle correspondant à x= 0 ? Aides-toi éventuellement d'un schéma pour mieux comprendre.
je ne sais pas comment déterminer z
Je t'ai réduit le schéma à l'essentiel utile pour obtenir l'expression de z en fonction de x et
.
Go désigne la position du centre d'inertie du solide dans le cas particulier de l'équilibre. Son altitude est choisie arbitrairement nulle. G désigne la position du centre d'inertie du solide à une date "t" quelconque. L'abscisse de G est ainsi : x=GoG, valeur positive sur la figure. L'altitude z de G est aussi l'altitude de H.
Je te laisse exprimer z en fonction de x et de
. Attention au signe !
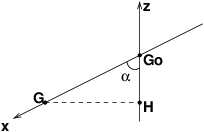
Merci beaucoup je trouve avec cette schéma
Que cos(alpha)=-z/x car z allonge sur le sens négatif et x sur le sens positif par suite on trouve que Epp = 1/2 kx^2 et Em = 1/2kx^2 +1/2 mv^2. Comme ça?
Annuler
connectez vous