Inscription / Connexion Nouveau Sujet
Pendule de torsion 1
Bonsoir, svp guidez moi
Problème
Un ressort spiral de masse négligeable, de constante C est fixé en O par une extrémité. L'autre extrémité est liée à un arbre de masse négligeable d'axe (
). Une roue de moment d'inertie Jo par rapport à l'axe et centré sur celui-ci est solidaire de l'arbre (voir croquis).
1) Montrer que le système écarté de sa position d'équilibre d'un angle 
m puis libéré sans vitesse est animé d'un mouvement sinusoïdal de rotation.
2) La période des oscillations du pendule précédent est T1 = 1,20 s. Cette période devient égale à T2 = 1,42 s lorsqu'on surcharge la roue de deux masselottes identiques m = 20 g placées sur le même diamètre de part et d'autre de l'axe de rotation et à 5 cm de celui-ci. Calculer Jo et C.
3) On retire les deux masselottes, on fait osciller le pendule avec une amplitude de 90⁰.
Pour quelle valeur de l'élongation angulaire l'énergie potentielle élastique du système est-elle égale à l'énergie cinétique ?
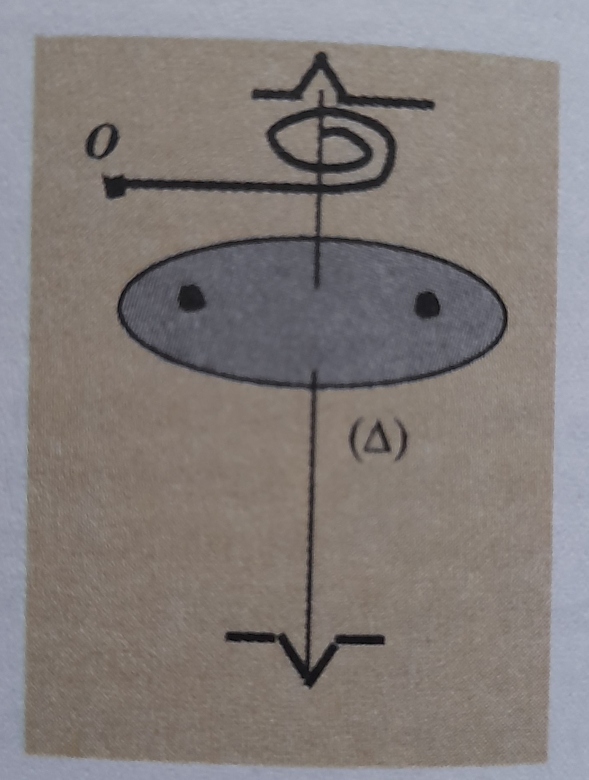
Aidez d'abord à comprendre le schéma, c'est là je suis bloqué d'abord.
Quand on dit que la roue est solidaire à l'arbre, qu'est-ce cela signifie ?
Ensuite, écarté le système de sa position d'équilibre revient à faire tourner la roue autour de l'axe ? Ou alors la roue et l'axe sont soudés ensemble, c'est-à-dire ont la même vitesse ?
Ou alors la roue et l'axe sont soudés ensemble
Oui, donc quand l'arbre tourne dun angle
, la roue aussi.Bonjour krinn, bonjour tout le monde.
J'ai beau analyser cet exercice, mais j'avoue honnêtement que j'ai du mal à l'aborder.
Veuillez me guider un peu, svp.
Bonsoir,
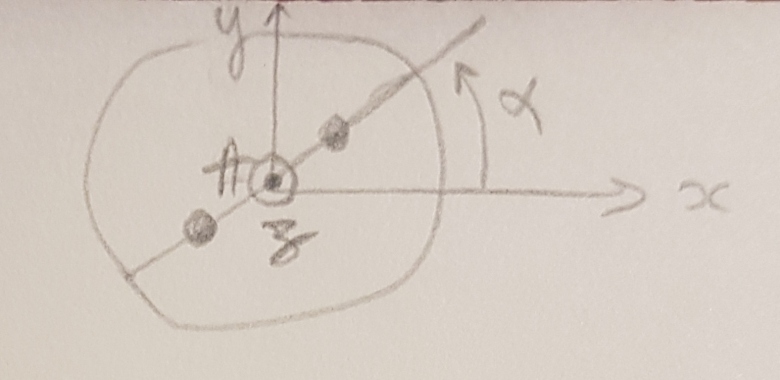
Avec une vue de dessus, et en utilisant le paramètre de position angulaire , ce sera peut-être plus clair (cf. schéma)
L'axe de rotation ( ) correspond à (Az) sur le dessin.
Je crois que je dois appliquer le "Théorème de l'accélération angulaire" sur la roue.
Je fais d'abord le bilan des forces :
- Le poids de la roue ;
- le couple de rappel de moment 
c exercé par le ressort spiral sur la roue.
Alors 
= J" 
Or car le poids rencontre l'axe
c = - C. est le moment du couple.
Alors J'obtiens enfin : J0" + C = 0
Avec J = J0 est le moment d'inertie de la roue.
Plus simplement :
c'est l'équation différentielle du mouvement caractéristique des mouvements sinusoïdaux de rotation.
C'est ça ?
Bonjour,
Je crois que je dois appliquer le "Théorème de l'accélération angulaire" sur la roue.
Je fais d'abord le bilan des forces :
- Le poids
- le couple de rappel de moment
c exercé par le ressort spiral sur la roue.En fait ici il faut considerer le systeme {arbre + roue} qui forme un solide en rotation soumis à un couple, à son poids ET ....
Attention à ne pas oublier de force! En general, ca ne pardonne pas en meca.
Ceci dit, ici, ca ne change pas le resultat que tu as trouvé qui est bon (si on neglige les frottements et si l'arbre a une masse negligeable) , mais c'est un coup de chance !
D'accord.
Donc dans le bilan des forces il faut tenir compte de la force qui compense l'effet du poids de la roue. Cette force est verticale ascendante, donc opposée au poids.
De toute façon, son moment est aussi nul, puisque la force rencontre l'axe
Oui, cette force s'appelle la reaction du support (ou plus generalement la ou les reactions de liaison)
D'accord, j'ai bien compris !
2) Calculons J0 et C
• En l'absence des deux masselottes, la pulsation est 
1² = C/J0 T1² = 4
².J0/C
Je garde cette relation
• En présence des deux masselottes, si je comprend bien, je dois chercher l'expression de nouvelle équation différentielle (toujours en fonction de J0 et C). En tenant compte des poids et
des deux masselottes, de moments respectifs
1 et 2 non nuls.
Ensuite, J'obtiens une nouvelle pulsation 2, du coup une nouvelle période T2 qui est fonction de J0 et C. C'est la 2ème relation.
Enfin je combine ces deux relations et je déduis J0 et C.
C'est ça ?
Effectivement, P1 et P2 ont un moment par rapport au centre du disque, mais la somme de ces moments est ....
En revanche quelle grandeur du systeme change si on ajoute les masselottes?
Le moment d'inertie J0 de la roue dépend de la masse de la roue et de la position de l'arbre .
Ici l'arbre est solidaire à la roue, donc si on ajoute les masselottes, la masse de la roue augmente,
donc J0 change.
Pour répondre à votre question, et
constituent deux forces parallèles de même sens, même norme et à égale distance de l'axe. L'effet de
sur la roue compense celui de
et inversement. Donc la somme de leurs moments est nulle.
Le moment d'inertie J0 de la roue dépend de la masse de la roue et de la position de l'arbre
.
Oui
Ici l'arbre est solidaire à la roue, donc si on ajoute les masselottes, la masse de la roue augmente et la distribution des masses change,
donc J0 change.
Oui
Jo devient J1 = Jo + .....
Pour répondre à votre question,
L'effet Le moment de
en revanche
D'accord mon cher. Je retiens ce que tu m'avais dit !
Ici chaque masselotte est assimilable à un point matériel de masse m tournant autour de l'arbre.
Tu m'avais dit qu'un point matériel tournant autour d'un point ou d'un axe a aussi un moment d'inertie 
noté J = mr² où r est le rayon de sa trajectoire.
Donc ici les deux masselottes étant identiques, la somme de leurs moments est J = 2mr²
Du coup le moment d'inertie de la roue devient :
J1 = J0 + 2mr²
D'accord, donc la nouvelle équation différentielle devient
Du coup
En fin je combine les relations T1 et T2 pour avoir J0 et C.
C'est ça ?
2,5.10-4 kg.m²
Oui, mais quelle est l'unité pour un couple?
kg.m².s-2 est juste physiquement mais pas tres pratique, on utilise plutôt le ....
Merci.
Question 3 :
• L'énergie potentielle élastique du ressort spiral est Epe = ½C²
• L'énergie cinétique du système est Ec = ½Jo²
Or = d/dt avec = m.cos(ot + 
)
En prenant l'origine des temps l'instant où le système est abandonné à lui-même ( = m = 90⁰), alors = 0⁰
Alors l'équation horaire est = m.cosot
Donc = d/dt = -mo.sinot
Ainsi Ec = ½Jom²o².sin²ot
Maintenant je dois poser que Epe = Ec, pour déterminer . Mais l'Ec varie en fonction du temps.
Est-ce que je peux utiliser directement la relation Ec = ½Jo², sachant que = 1 ?
Question 3 :
• L'énergie potentielle élastique du ressort spiral est Epe = ½C
²
• L'énergie cinétique du système est Ec = ½Jo
²
Oui, tres bien.
Or
= d/dt avec = m.cos(ot + )Attention! il y a une condition pour pouvoir ecrire ca. Et elle n'est pas remplie ici!
Maintenant je dois poser que Epe = Ec, pour déterminer
. Mais l'Ec varie en fonction du temps.
Oui, mais on sait autre chose sur l'energie mecanique du système...
• Quelle est la condition pour écrire = d/dt ?
• Ici l'Em se conserve, donc sa dérivée par rapport au temps est nulle.
Em = Epe + Ec
Mais je ne vois pas comment aboutir en utilisant l'énergie mécanique
• Quelle est la condition pour écrire
= d/dt ?
Aucune, c'est la definition, mais c'est
(t) qui pose probleme.
• Ici l'Em se conserve, donc sa dérivée par rapport au temps est nulle.
Em = Epe + Ec
Oui, Em est constante et donc connue puisqu'on connait les conditions initiales, donc Em=Eo = Ec + Epe à tout instant
Donc, si je comprend bien, je dois poser que :
• A l'instant initial : = 0 et = m = 90⁰
L'origine des temps est choisie à l'instant où le système est abandonné sans vitesse.
Ainsi Em = ½Cm² puisque Ec = 0
• A un instant t quelconque Ec = Epe
Or Em = Ec + Epe
Donc Em = 2.Epe
Or l'Em se conserve, donc j'égalise les deux expressions de l'Em :
½Cm² = 2.½C² = m/
2
AN : = 31,8⁰
C'est ça ?
Le raisonnement est bon.
Mais la valeur de n'est pas bonne,
et Ec=Epe uniquement à un certain instant (qu on ne sait pas calculer ici), et non pas à un instant quelconque.
Pourquoi (t) 
m cos(t + ) dans cette question?
Oups, jai dit une betise : ici on a un pendule de torsion, donc l'eq. diff.
Jo" + C = 0 est tjs valable meme pour "grand"
Donc (t) = m cos(t + )
J'ai confondu avec le pendule simple.
Il est risqué de vouloir faire de la physique pendant les fetes!
Toutefois la methode energetique est nettement plus simple pour la question 3).
Ah d'accord, j'ai commis une erreur d'application numérique !
= m/2
AN : m = 90⁰ , je trouve = 63,6⁰
Annuler
connectez vous