Inscription / Connexion Nouveau Sujet
Pb de condensateur
Voilà le "ptit" problème:

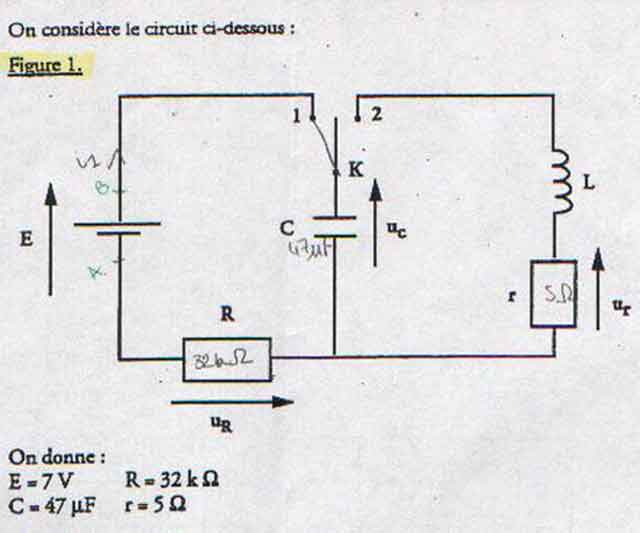
On étudie la charge d'un condensateur de capacité C par un générateur de tension, de force électromotrice E, à travers un circuit de résistance R ( figure 1 ). A l'instant t=0 s, on ferme l'interrupteur K en 1 et, à l'aide d'un ordinateur muni d'une carte d'acquisition de données, on enregistre l'évolution au cours du temps de la tension Uc aux bornes du condensateur, ainsi que la tension Ur aux bornes du conducteur ohmique, comme l'inidque le doc. A .
1.a) Quelle est, de C1 ou de C2, la courbe représentative de Uc ?
b. Comment pourrai-on obtenir la courbe représentative du courant i circualant ds le circuit?
=> La c2 car sur le graphe, elle est croissanceet Uab = E
2.a) A l'instant t=5s, le condensateur a-t-il atteint sa charge maximale?? Justifie
b. Quelle sera la tension aux bornes de C en fin de charge? Justifier
3.a) Sachant que la constante de temps T est la durée au bout de laquelle le condensateur a acquis 63% de sa charge maximale, déterminer graphiquement la valeur de T.
b.Le résultat trouvé est-il en accord avec la valeur déduite de son expression théorique; T=RC
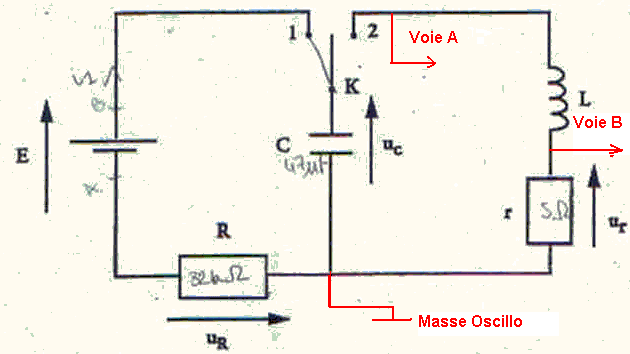
B. Le condensateur ayant acquis sa charge maximale, on bascule K en 2. On observe alors avec un oscilloscope sur la voie A la tension Uc aux bornes du condensateur et sur la voie B la tention Ur aux bornes de la résistance r.
Les réglages de l'oscilloscope:
Durée de balayage horizontale:5 ms/division
Sensibilité verticale voie A:2V/division
Sensibilité verticale voie B: 500 mV/division
1) Recopier la shéma du circuit en plaçant les 3 fils de liaison avec l'oscilloscope.
a. Justifier qualitativement la variation de l'amplitude des oscillations.
b. Tracer sommairement l'allure de Uc si r est très élevée.
3.a) Détermnier la pseudo-période T des oscillations.
b. En déduire une valeur approchéee de l'inductance L de la bobine, sachant que T= 2
 LxC
LxC
4.a) Rappeler les expressions qui donnent:
- l'energie Ec stockée ds le condensateur
- l'énergie stockée dans la bobine
b. Sur l'oscillogramme, on a repéré deux points M et N. Valculer l'énergie totale du circuit en chacun de ces points.
=> E=E condensateur + E bobine
E=1/2 C Uc ²+1/2 Li²
Le reste, je n'y parviens pas et c'est pas faute d'avoir cherché.
Merci bcp par avance
Les questions ne sont pas très compliquées, mais pour y répondre, il faut impérativement les dessins qui les accompagnent.
Essaie de les envoyer.

oui mais je n'ai pas pu accompagner l'exercice des courbes car les documents faisaient plus de 30 ko 
Essaie de mettre les dessins dans le logiciel "Paint" et de les sauver sous le format .gif, cela prend moins de place.
Si c'est encore trop grand, essaie d'enlever (avec Paint), toutes les parties non nécessaires des images. (cadres ...).
Tu peux aussi essayer d'envoyer dans 2 réponses séparées les 2 images que tu as probablement pour l'exercice.
Sans cela, je ne pourrai pas t'aider.

Pour les courbes, le site bug car mon document fait 27.1 Ko et de dimensions 417 x 640 et on me dit que le document ne doit pas dépasser 650x600 dc y'a un soucis et je suis ds la mouisse 
slt
1-a)on étudie la charge du condensateur donc U croît et donc la courbe représentative de Uc est ou autre justification a l'instant t=0 la tension Uc aux bornes du condensateur vaut 0 car décharger donc si x=0 Uc=0 ce qui est verifié par
2)a)
La constante de temps RC = 32000 * 47.10^-6 = 1,5 s
en 5 secondes, soit 3,33 constantes de temps RC, la tension aux bornes du condensateur est très proche de son maximum mais n'y est pas encore tout à fait.
b)
En fin de charge, la tension aux bornes du condensateur sera = 7 volts (soit la valeur de E).
En effet, à la fin de la charge, le courant de charge est nul, il n'y a donc plus de chute de tension aux bornes de R.
La tension de E se retrouve donc alors aux bornes du condensateur.
-----
3)
a)
63% de 7 volts = 4,41 volts.
Sur la courbe 1, on a la courbe C2 qui passe à 4,41 volts pour t = 1,5 s.
Donc graphiquement, la constante de temps T = 1,5 s
b)
Oui, car on a RC = 32000 * 47.10^-6 = 1,5 s
----------
B)
1) Voir dessin.
b) Si r est très élevée, la tension aus bornes du condensateur sera approximativement de la forme: Vc = 7.e^(-rC), soit une exponentielle décroissante de constante de temps = rC.
-----
Pour la question 3, il manque de nouveau un dessin.
-----
4)
a)
Ec = (1/2).C.(Uc)²
EL = (1/2).L.i²
---
b)
Il manque un dessin pour pouvoir répondre.
-----
Merci ! J'avais pas vu ça comme ça... je pensais que la charge était croissance mais non puisque Uc =0 Logique en plus
Merci !
I-
2-a) trace la tangente a l'origine et l'asymptote a la courbe tu determine ainsi or on sait que le condensateur est charger a
...
b) En fin de charge Uc=E regarde les courbes fournit et par identification de celle ci tu pourra le deduire
3-a)Determine E a l'aide du graphique et fait 0,63E que tu porte en ordonnée pour deduire l'absisse de : tu devrai normalement retrouvé la valeur obtenu graphiquement precedemment
b) d'une part on trouve T en faisan 0,63E et d'autre part on le détermine par le calcul : regarde si ca coincide
Suite et fin.
3)a)
La pseudo période est: 2*5ms = 10 ms
b) 10^-2 = 2.Pi. racinecarrée(L.47.10^-6)
10^-4 = 4.Pi².47.10^-6.L
L = 100/(47.4.Pi²)
L = 0,054 Henry environ
-----
4)
b)
En M:
Uc = 4,4 volts
ur = 0 -> i = 0
Ec = (1/2)*47.10^-6*4,4² = 4,55.10^-4 Joule
EL = (1/2)*0,054*0² = 0 Joule
E = Ec + EL = 4,55.10^-4 Joule
---
en N:
uc = 0 -> Ec = 0
ur = 1,2 * 0,5 = 0,6 volt, avec r = 5 Ohm -> i = 0,6/5 = 0,12 A
EL = (1/2)*0,054*0,12² = 3,9.10^-4 Joule.
E = Ec + EL = 3,9.10^-4 Joule.
-----
Sauf distraction. 
Merci au correcteur J-P ainsi qu'à H_aldnoer pr leurs aides !!
Pr quelques questions, une fois amorcé, c'était tout de suite bcp plus simple mais pr d'autres  ouhlala !
ouhlala !
Merci bcp et bonne apres-midi à vous 
Je vous met  pour votre rapidité!!
pour votre rapidité!!
Chicane